| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Class 6th Chapters | ||
|---|---|---|
| 1. Number System | 2. Geometry | 3. Integers |
| 4. Fractions & Decimals | 5. Data Handling | 6. Mensuration |
| 7. Algebra | 8. Ratio & Proportion | 9. Symmetry & Practical Geometry |
Chapter 8 Ratio & Proportion
Welcome to this detailed resource centre, offering comprehensive solutions for the NCERT Exemplar problems specifically curated for Class 6 Mathematics, Chapter 8: Ratio & Proportion. It is vital to understand that these Exemplar questions are meticulously crafted to extend beyond standard textbook exercises. They aim to significantly deepen students' conceptual grasp of comparing quantities using ratios, understanding the equivalence inherent in proportions, and skillfully applying the unitary method. This is achieved through presenting more complex scenarios, intricate word problems, and application-oriented tasks that demand more than just rote memorization of formulas.
The solutions provided here thoroughly address the fundamental concepts underpinning ratio and proportion. Key aspects covered include:
- Understanding Ratio: Grasping ratio as a fundamental method for comparing two quantities by division (often written as $a:b$ or $\frac{a}{b}$). Emphasis is placed on ensuring quantities are in the same units before forming a ratio, often requiring explicit unit conversions.
- Simplifying Ratios: Expressing ratios in their simplest form by dividing both terms by their Highest Common Factor (HCF).
- Comparing Ratios: Developing methods to determine which of two or more ratios is greater, especially when dealing with numerically close ratios. This involves techniques like converting them to like fractions (using LCM of denominators) or using cross-multiplication.
Moving beyond simple comparison, the solutions delve into the concept of proportion:
- Understanding Proportion: Recognizing proportion as a statement of equality between two ratios. If the ratio $a:b$ is equal to the ratio $c:d$, we say $a, b, c, d$ are in proportion, often written as $a:b :: c:d$ or equivalently, $\frac{a}{b} = \frac{c}{d}$. Here, $a$ and $d$ are called the extremes, while $b$ and $c$ are called the means.
- Checking for Proportion: Applying the fundamental property of proportions: four quantities $a, b, c, d$ are in proportion if and only if the product of the extremes equals the product of the means, i.e., $a \times d = b \times c$.
- Solving Proportions: Finding a missing term in a proportion when the other three terms are known, using the relationship $ad = bc$.
A significant part of this chapter involves practical problem-solving using the Unitary Method. The solutions guide students through:
- The core logic: First finding the value corresponding to one unit of a quantity, and then using that value to calculate the value corresponding to the required number of units.
- Multi-step problems: Applying the method in scenarios requiring several steps or intermediate calculations.
- Complex calculations: Handling situations where finding the value of 'one unit' might involve fractions or decimals, demanding careful computation. Common applications involve calculating costs (potentially using the $\textsf{₹}$ symbol), distances, time, or quantities consumed/produced.
The Exemplar problems test these concepts rigorously through various formats, fully addressed by our solutions: MCQs assessing conceptual clarity, Fill-in-the-Blanks needing precise terms, True/False statements checking rules, and Short/Long Answer questions demanding detailed calculations or problem-solving narratives. Examples include solving proportion problems phrased in complex language or applying the unitary method where the 'per unit' calculation isn't straightforward. The solutions offer clear, step-by-step workings, explicitly showing methods like LCM for comparison, demonstrating the systematic application of the unitary method, highlighting necessary unit conversions, and providing logical interpretations of word problems. Engaging with this resource will empower students to master ratio and proportion concepts, sharpen their problem-solving skills using the unitary method, and apply these essential mathematical tools effectively across diverse quantitative situations.
Solved Examples (Examples 1 to 8)
In examples 1 and 2, write the correct answer from the given four options:
Example 1. The ratio of Rs 8 to 80 paise is
(A) 1 : 10
(B) 10 : 1
(C) 1: 1
(D) 100 : 1
Answer:
To find the ratio of two quantities, they must be in the same unit.
The given quantities are $\textsf{₹} 8$ and 80 paise.
We need to convert one of the quantities so that both are in the same unit (either Rupees or paise).
We know that 1 Rupee = 100 paise.
So, $\textsf{₹} 8 = 8 \times 100$ paise = 800 paise.
Now we find the ratio of 800 paise to 80 paise.
Ratio $= \frac{\text{Quantity 1}}{\text{Quantity 2}} = \frac{800 \text{ paise}}{80 \text{ paise}}$
Ratio $= \frac{800}{80}$
We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 80.
Ratio $= \frac{\cancel{800}^{10}}{\cancel{80}_{1}} = \frac{10}{1}$
The ratio can be written as 10 : 1.
Comparing this with the given options:
(A) 1 : 10
(B) 10 : 1
(C) 1 : 1
(D) 100 : 1
The correct option is (B) 10 : 1.
Example 2. The length and breadth of a steel tape are 10m and 2.4cm, respectively. The ratio of the length to the breadth is
(A) 5 : 1.2
(B) 25 : 6
(C) 625 : 6
(D) 1250 : 3
Answer:
To find the ratio of two quantities, they must be in the same unit.
The given quantities are:
Length = 10 m
Breadth = 2.4 cm
We need to convert one of the quantities so that both are in the same unit. It is easiest to convert meters to centimeters.
We know that 1 meter = 100 centimeters.
So, Length = $10 \text{ m} = 10 \times 100 \text{ cm} = 1000 \text{ cm}$.
Breadth = 2.4 cm.
Now we find the ratio of the length to the breadth:
Ratio $= \frac{\text{Length}}{\text{Breadth}} = \frac{1000 \text{ cm}}{2.4 \text{ cm}} = \frac{1000}{2.4}$
To remove the decimal from the denominator, multiply both the numerator and the denominator by 10:
Ratio $= \frac{1000 \times 10}{2.4 \times 10} = \frac{10000}{24}$
Now, simplify the fraction by dividing both the numerator and the denominator by common factors. Both are divisible by 2, then 2 again, and then 2 again.
$\frac{10000}{24} = \frac{\cancel{10000}^{5000}}{\cancel{24}_{12}} = \frac{\cancel{5000}^{2500}}{\cancel{12}_{6}} = \frac{\cancel{2500}^{1250}}{\cancel{6}_{3}} = \frac{1250}{3}$
The simplified ratio is $\frac{1250}{3}$, which is written as 1250 : 3.
Comparing this with the given options:
(A) 5 : 1.2 corresponds to $\frac{5}{1.2} = \frac{50}{12} = \frac{25}{6}$.
(B) 25 : 6 corresponds to $\frac{25}{6}$.
(C) 625 : 6 corresponds to $\frac{625}{6}$.
(D) 1250 : 3 corresponds to $\frac{1250}{3}$.
The correct option is (D) 1250 : 3.
Example 3. Find the missing number in the box in the following proportion:
⬜ : 8 :: 12 : 32
Answer:
A proportion is an equality of two ratios. The statement $\Box : 8 :: 12 : 32$ means that the ratio of the number in the box to 8 is equal to the ratio of 12 to 32.
We can write this proportion as an equation of fractions:
$\frac{\text{Missing Number}}{8} = \frac{12}{32}$
Let the missing number be represented by $x$. The equation becomes:
$\frac{x}{8} = \frac{12}{32}$
To solve for $x$, we can multiply both sides of the equation by 8:
$x = \frac{12}{32} \times 8$
$x = \frac{12 \times 8}{32}$
$x = \frac{96}{32}$
Now, we perform the division:
$96 \div 32 = 3$
So, $x = 3$.
Alternatively, we could simplify the fraction $\frac{12}{32}$ first. Both 12 and 32 are divisible by 4:
$\frac{12}{32} = \frac{12 \div 4}{32 \div 4} = \frac{3}{8}$
The equation becomes:
$\frac{x}{8} = \frac{3}{8}$
Since the denominators are equal, the numerators must also be equal for the fractions to be equivalent.
Thus, $x = 3$.
The missing number in the proportion is 3.
Example 4. State whether the given statements are true or false:
(a) 12 : 18 = 28 : 56
(b) 25 persons : 130 persons = 15kg : 78kg
Answer:
To check if two ratios are equal (i.e., if they form a proportion), we can simplify each ratio to its lowest terms or check if the product of the means equals the product of the extremes.
(a) 12 : 18 = 28 : 56
Let's simplify each ratio:
Ratio 1: 12 : 18 = $\frac{12}{18}$
Both 12 and 18 are divisible by 6.
$\frac{12}{18} = \frac{12 \div 6}{18 \div 6} = \frac{2}{3}$
Ratio 2: 28 : 56 = $\frac{28}{56}$
Both 28 and 56 are divisible by 28.
$\frac{28}{56} = \frac{28 \div 28}{56 \div 28} = \frac{1}{2}$
Since $\frac{2}{3} \neq \frac{1}{2}$, the statement is false.
Alternatively, using the product of means and extremes:
For 12 : 18 = 28 : 56 to be true, the product of the means (18 and 28) must equal the product of the extremes (12 and 56).
Product of means = $18 \times 28$
$\begin{array}{cc}& & 1 & 8 \\ \times & & 2 & 8 \\ \hline & 1 & 4 & 4 \\ 3 & 6 & \times \\ \hline 5 & 0 & 4 \\ \hline \end{array}$
Product of means = 504.
Product of extremes = $12 \times 56$
$\begin{array}{cc}& & 1 & 2 \\ \times & & 5 & 6 \\ \hline & & 7 & 2 \\ 6 & 0 & \times \\ \hline 6 & 7 & 2 \\ \hline \end{array}$
Product of extremes = 672.
Since $504 \neq 672$, the statement is false.
Statement (a) is False.
(b) 25 persons : 130 persons = 15kg : 78kg
The units ('persons' and 'kg') cancel out when forming the ratios.
Let's simplify each ratio:
Ratio 1: 25 : 130 = $\frac{25}{130}$
Both 25 and 130 are divisible by 5.
$\frac{25}{130} = \frac{25 \div 5}{130 \div 5} = \frac{5}{26}$
Ratio 2: 15 : 78 = $\frac{15}{78}$
Both 15 and 78 are divisible by 3.
$\frac{15}{78} = \frac{15 \div 3}{78 \div 3} = \frac{5}{26}$
Since $\frac{5}{26} = \frac{5}{26}$, the statement is true.
Alternatively, using the product of means and extremes:
For 25 : 130 = 15 : 78 to be true, the product of the means (130 and 15) must equal the product of the extremes (25 and 78).
Product of means = $130 \times 15$
$130 \times 15 = 130 \times (10 + 5) = 1300 + 650 = 1950$
Product of means = 1950.
Product of extremes = $25 \times 78$
$\begin{array}{cc}& & 2 & 5 \\ \times & & 7 & 8 \\ \hline & 2 & 0 & 0 \\ 17 & 5 & \times \\ \hline 19 & 5 & 0 \\ \hline \end{array}$
Product of extremes = 1950.
Since $1950 = 1950$, the statement is true.
Statement (b) is True.
Example 5. Fill in the blanks:
If two ratios are ______, then they are in proportion.
Answer:
The definition of a proportion is an equality between two ratios.
Therefore, if two ratios are equal, they form a proportion.
Filling in the blank:
If two ratios are equal, then they are in proportion.
Example 6. Find the ratio of the shaded portion to the unshaded portion in Fig. 8.1

Answer:
The image shows a grid of squares.
We need to count the number of shaded squares and the number of unshaded squares.
Number of shaded squares = 5
Number of unshaded squares = 30
The ratio of the shaded portion to the unshaded portion is given by:
Ratio = $\frac{\text{Number of shaded squares}}{\text{Number of unshaded squares}} = \frac{5}{30}$
To express the ratio in its simplest form, we divide both the numerator and the denominator by their greatest common divisor, which is 5.
Ratio $= \frac{\cancel{5}^{1}}{\cancel{30}_{6}} = \frac{1}{6}$
The ratio of the shaded portion to the unshaded portion is $\mathbf{1 : 6}$.
Example 7. Income of Rahim is Rs 12000 per month and that of Ami is Rs 191520 per annum. If the monthly expenditure of each of them is Rs 9960 per month find the ratio of their savings.
Answer:
To find the ratio of their savings, we first need to calculate the monthly savings for both Rahim and Amit.
Savings = Income - Expenditure.
We must ensure that both income and expenditure are for the same time period (monthly in this case).
Rahim's Savings:
Rahim's monthly income = $\textsf{₹} 12000$
Rahim's monthly expenditure = $\textsf{₹} 9960$
Rahim's monthly savings = Rahim's monthly income - Rahim's monthly expenditure
Rahim's monthly savings = $\textsf{₹} 12000 - \textsf{₹} 9960$
$\begin{array}{cc} & 1 & 2 & 0 & 0 & 0 \\ - & & 9 & 9 & 6 & 0 \\ \hline & & 2 & 0 & 4 & 0 \\ \hline \end{array}$
Rahim's monthly savings = $\textsf{₹} 2040$.
Amit's Savings:
Amit's annual income = $\textsf{₹} 191520$
We need to find Amit's monthly income. There are 12 months in a year.
Amit's monthly income = Amit's annual income $\div$ 12
Amit's monthly income = $\textsf{₹} 191520 \div 12$
$\begin{array}{r} 15960\phantom{)} \\ 12{\overline{\smash{\big)}\,191520\phantom{)}}} \\ \underline{-~\phantom{(}(12)\phantom{0000)}} \\ 71\phantom{000)} \\ \underline{-~\phantom{()}(60)\phantom{000)}} \\ 115\phantom{00)} \\ \underline{-~\phantom{()}(108)\phantom{00)}} \\ 72\phantom{0)} \\ \underline{-~\phantom{()}(72)\phantom{0)}} \\ 00 \\ \underline{-~\phantom{()}(00)} \\ 0 \end{array}$
Amit's monthly income = $\textsf{₹} 15960$.
Amit's monthly expenditure = $\textsf{₹} 9960$
Amit's monthly savings = Amit's monthly income - Amit's monthly expenditure
Amit's monthly savings = $\textsf{₹} 15960 - \textsf{₹} 9960$
$\begin{array}{cc} & 1 & 5 & 9 & 6 & 0 \\ - & & 9 & 9 & 6 & 0 \\ \hline & & 6 & 0 & 0 & 0 \\ \hline \end{array}$
Amit's monthly savings = $\textsf{₹} 6000$.
Now, we find the ratio of their savings (Rahim's savings : Amit's savings).
Ratio = $\frac{\text{Rahim's savings}}{\text{Amit's savings}} = \frac{\textsf{₹} 2040}{\textsf{₹} 6000} = \frac{2040}{6000}$
Simplify the ratio by dividing the numerator and denominator by common factors:
$\frac{2040}{6000} = \frac{204}{600} = \frac{51}{150} = \frac{17}{50}$
The ratio of their savings is 17 : 50.
The ratio of their savings is 17 : 50.
Example 8. 20 tons of iron costs Rs 600000. Find the cost of 560kg of iron.
Answer:
We are given the cost of a certain amount of iron in tons and need to find the cost of an amount given in kilograms.
First, we need to convert the given quantities to the same unit. We know that 1 ton = 1000 kg.
Given:
Quantity of iron = 20 tons
Cost of 20 tons of iron = $\textsf{₹} 600000$
We need to find the cost of 560 kg of iron.
Convert the quantity from tons to kilograms:
20 tons = $20 \times 1000 \text{ kg} = 20000 \text{ kg}$.
So, the cost of 20000 kg of iron is $\textsf{₹} 600000$.
We can use the unitary method or proportion to find the cost of 560 kg.
Using the unitary method:
Cost of 20000 kg of iron = $\textsf{₹} 600000$
Cost of 1 kg of iron = $\frac{\text{Cost of 20000 kg}}{\text{Quantity in kg}} = \frac{\textsf{₹} 600000}{20000}$
Cost of 1 kg = $\frac{\textsf{₹} 600000}{20000} = \frac{\cancel{600000}^{600}}{\cancel{20000}_{20}} = \frac{600}{20} = \frac{60}{2} = \textsf{₹} 30$.
The cost of 1 kg of iron is $\textsf{₹} 30$.
Now, find the cost of 560 kg of iron:
Cost of 560 kg = (Cost of 1 kg) $\times$ (Quantity in kg)
Cost of 560 kg = $\textsf{₹} 30 \times 560$
$30 \times 560 = 3 \times 5600 = 16800$
Cost of 560 kg = $\textsf{₹} 16800$.
Using proportion:
Let the cost of 560 kg of iron be $\textsf{₹} C$. The ratio of quantity to cost should be constant.
$\frac{\text{Quantity 1}}{\text{Cost 1}} = \frac{\text{Quantity 2}}{\text{Cost 2}}$
$\frac{20000 \text{ kg}}{\textsf{₹} 600000} = \frac{560 \text{ kg}}{\textsf{₹} C}$
$\frac{20000}{600000} = \frac{560}{C}$
$\frac{20}{600} = \frac{560}{C}$
$\frac{1}{30} = \frac{560}{C}$
Cross-multiply:
$1 \times C = 30 \times 560$
$C = 16800$
The cost of 560 kg of iron is $\textsf{₹} 16800$.
The cost of 560kg of iron is $\textsf{₹} 16800$.
Exercise
Question 1 to 10 (Multiple Choice Questions)
In questions 1 to 10, only one of the four options is correct. Write the correct one.
Question 1. The ratio of 8 books to 20 books is
(A) 2 : 5
(B) 5 : 2
(C) 4 : 5
(D) 5 : 4
Answer:
We need to find the ratio of 8 books to 20 books.
Ratio $= \frac{\text{Quantity 1}}{\text{Quantity 2}} = \frac{8 \text{ books}}{20 \text{ books}}$
Since the units are the same, they cancel out.
Ratio $= \frac{8}{20}$
To simplify the fraction, we find the greatest common divisor (GCD) of 8 and 20, which is 4.
Divide both the numerator and the denominator by 4:
Ratio $= \frac{8 \div 4}{20 \div 4} = \frac{2}{5}$
The ratio can be written as 2 : 5.
Comparing this with the given options:
(A) 2 : 5
(B) 5 : 2
(C) 4 : 5
(D) 5 : 4
The correct option is (A) 2 : 5.
Question 2. The ratio of the number of sides of a square to the number of edges of a cube is
(A) 1 : 2
(B) 3 : 2
(C) 4 : 1
(D) 1 : 3
Answer:
We need to find the ratio of the number of sides of a square to the number of edges of a cube.
Number of sides of a square:
A square is a two-dimensional shape with 4 straight sides.
Number of sides of a square = 4.
Number of edges of a cube:
A cube is a three-dimensional shape. Edges are the lines where two faces meet.
A cube has 12 edges.
The ratio of the number of sides of a square to the number of edges of a cube is:
Ratio $= \frac{\text{Number of sides of a square}}{\text{Number of edges of a cube}} = \frac{4}{12}$
To simplify the fraction, we find the greatest common divisor (GCD) of 4 and 12, which is 4.
Divide both the numerator and the denominator by 4:
Ratio $= \frac{4 \div 4}{12 \div 4} = \frac{1}{3}$
The ratio can be written as 1 : 3.
Comparing this with the given options:
(A) 1 : 2
(B) 3 : 2
(C) 4 : 1
(D) 1 : 3
The correct option is (D) 1 : 3.
Question 3. A picture is 60cm wide and 1.8m long. The ratio of its width to its perimeter in lowest form is
(A) 1 : 2
(B) 1 : 3
(C) 1 : 4
(D) 1 : 8
Answer:
To find the ratio, the quantities must be in the same unit.
Given:
Width of the picture = 60 cm
Length of the picture = 1.8 m
Convert the length from meters to centimeters. We know that $1 \text{ m} = 100 \text{ cm}$.
Length $= 1.8 \text{ m} = 1.8 \times 100 \text{ cm} = 180 \text{ cm}$.
The picture is rectangular. The perimeter of a rectangle is given by the formula $P = 2(\text{length} + \text{width})$.
Perimeter $= 2(180 \text{ cm} + 60 \text{ cm})$
Perimeter $= 2(240 \text{ cm})$
Perimeter $= 480 \text{ cm}$.
We need to find the ratio of the width to the perimeter.
Ratio $= \frac{\text{Width}}{\text{Perimeter}} = \frac{60 \text{ cm}}{480 \text{ cm}}$
Ratio $= \frac{60}{480}$
Simplify the fraction by dividing the numerator and the denominator by their greatest common divisor. Both are divisible by 60.
Ratio $= \frac{60 \div 60}{480 \div 60} = \frac{1}{8}$
The ratio in lowest form is 1 : 8.
Comparing the calculated ratio with the given options:
(A) 1 : 2
(B) 1 : 3
(C) 1 : 4
(D) 1 : 8
The correct option is (D) 1 : 8.
Question 4. Neelam’s annual income is Rs. 288000. Her annual savings amount to Rs. 36000. The ratio of her savings to her expenditure is
(A) 1 : 8
(B) 1 : 7
(C) 1 : 6
(D) 1 : 5
Answer:
We need to find the ratio of savings to expenditure. We are given the annual income and annual savings.
Expenditure = Income - Savings.
Given:
Annual income = $\textsf{₹} 288000$
Annual savings = $\textsf{₹} 36000$
Calculate her annual expenditure:
Annual expenditure = Annual income - Annual savings
Annual expenditure = $\textsf{₹} 288000 - \textsf{₹} 36000$
$\begin{array}{cc} & 2 & 8 & 8 & 0 & 0 & 0 \\ - & & 3 & 6 & 0 & 0 & 0 \\ \hline & 2 & 5 & 2 & 0 & 0 & 0 \\ \hline \end{array}$
Annual expenditure = $\textsf{₹} 252000$.
Now, find the ratio of her savings to her expenditure:
Ratio = $\frac{\text{Savings}}{\text{Expenditure}} = \frac{\textsf{₹} 36000}{\textsf{₹} 252000} = \frac{36000}{252000}$
Simplify the fraction. We can cancel out the three zeros from both numerator and denominator.
Ratio $= \frac{36}{252}$
Both 36 and 252 are divisible by 36 (since $252 = 7 \times 36$).
Ratio $= \frac{36 \div 36}{252 \div 36} = \frac{1}{7}$
The ratio of her savings to her expenditure is 1 : 7.
Comparing this with the given options:
(A) 1 : 8
(B) 1 : 7
(C) 1 : 6
(D) 1 : 5
The correct option is (B) 1 : 7.
Question 5. Mathematics textbook for Class VI has 320 pages. The chapter ‘symmetry’ runs from page 261 to page 272. The ratio of the number of pages of this chapter to the total number of pages of the book is
(A) 11 : 320
(B) 3 : 40
(C) 3 : 80
(D) 272 : 320
Answer:
We need to find the ratio of the number of pages in the 'symmetry' chapter to the total number of pages in the book.
Given:
Total number of pages in the book = 320.
The chapter 'symmetry' runs from page 261 to page 272.
To find the number of pages in the chapter, we subtract the starting page number from the ending page number and add 1 (to include both the start and end pages).
Number of pages in the chapter = (Ending page number) - (Starting page number) + 1
Number of pages in the chapter = $272 - 261 + 1$
$272 - 261 = 11$
$11 + 1 = 12$
Number of pages in the chapter = 12.
Now, find the ratio of the number of pages in the chapter to the total number of pages:
Ratio $= \frac{\text{Number of pages in chapter}}{\text{Total number of pages}} = \frac{12}{320}$
Simplify the fraction by dividing the numerator and the denominator by their greatest common divisor. Both are divisible by 4.
$\frac{12}{320} = \frac{12 \div 4}{320 \div 4} = \frac{3}{80}$
The ratio in lowest form is 3 : 80.
Comparing this with the given options:
(A) 11 : 320
(B) 3 : 40
(C) 3 : 80
(D) 272 : 320
The correct option is (C) 3 : 80.
Question 6. In a box, the ratio of red marbles to blue marbles is 7:4. Which of the following could be the total number of marbles in the box?
(A) 18
(B) 19
(C) 21
(D) 22
Answer:
The ratio of red marbles to blue marbles is given as 7:4.
This means that for every 7 red marbles, there are 4 blue marbles.
If we represent the number of red marbles as $7k$ and the number of blue marbles as $4k$, where $k$ is a positive integer, then the ratio is $\frac{7k}{4k} = \frac{7}{4}$.
The total number of marbles in the box would be the sum of the number of red marbles and the number of blue marbles.
Total marbles = Number of red marbles + Number of blue marbles
Total marbles $= 7k + 4k = 11k$.
This means that the total number of marbles must be a multiple of 11.
We need to check which of the given options is a multiple of 11.
- (A) 18: Is 18 a multiple of 11? No ($11 \times 1 = 11, 11 \times 2 = 22$).
- (B) 19: Is 19 a multiple of 11? No.
- (C) 21: Is 21 a multiple of 11? No.
- (D) 22: Is 22 a multiple of 11? Yes ($11 \times 2 = 22$).
If the total number of marbles is 22, then $11k = 22$, which means $k = \frac{22}{11} = 2$.
In this case, the number of red marbles would be $7k = 7 \times 2 = 14$, and the number of blue marbles would be $4k = 4 \times 2 = 8$. The ratio is $14 : 8$, which simplifies to $7 : 4$. The total number is $14 + 8 = 22$.
The total number of marbles in the box could be (D) 22.
Question 7. On a shelf, books with green cover and that with brown cover are in the ratio 2:3. If there are 18 books with green cover, then the number of books with brown cover is
(A) 12
(B) 24
(C) 27
(D) 36
Answer:
The ratio of books with green cover to books with brown cover is 2:3.
This means that for every 2 books with a green cover, there are 3 books with a brown cover.
Let the number of books with green cover be $G$ and the number of books with brown cover be $B$.
We are given the ratio $\frac{G}{B} = \frac{2}{3}$.
We are also given that the number of books with green cover is 18.
$G = 18$.
Substitute the value of $G$ into the ratio equation:
$\frac{18}{B} = \frac{2}{3}$
Now we solve for $B$. We can use cross-multiplication.
$18 \times 3 = 2 \times B$
$54 = 2B$
Divide both sides by 2:
$B = \frac{54}{2}$
$B = 27$
The number of books with brown cover is 27.
Alternatively, we can think of the ratio as representing parts. The ratio 2:3 means that the green books represent 2 parts and the brown books represent 3 parts.
If 2 parts correspond to 18 books,
Then 1 part corresponds to $\frac{18}{2} = 9$ books.
The brown books correspond to 3 parts.
Number of brown books = 3 parts $\times$ (books per part)
Number of brown books $= 3 \times 9 = 27$.
Comparing the result with the given options:
(A) 12
(B) 24
(C) 27
(D) 36
The correct option is (C) 27.
Question 8. The greatest ratio among the ratios 2 : 3, 5 : 8, 75 : 121 and 40 : 25 is
(A) 2 : 3
(B) 5 : 8
(C) 75 : 121
(D) 40 : 25
Answer:
To find the greatest ratio among the given ratios, we can convert each ratio into a fraction and then compare the fractions, for example, by converting them to decimals.
The given ratios are:
1. 2 : 3 = $\frac{2}{3}$
2. 5 : 8 = $\frac{5}{8}$
3. 75 : 121 = $\frac{75}{121}$
4. 40 : 25 = $\frac{40}{25}$
Let's convert these fractions into decimal form:
1. $\frac{2}{3} \approx 0.6666...$
2. $\frac{5}{8} = 0.625$
3. $\frac{75}{121} \approx 0.6198...$
4. $\frac{40}{25} = \frac{8}{5} = 1.6$
Now, comparing the decimal values:
$0.6666...$
$0.625$
$0.6198...$
$1.6$
The largest decimal value is 1.6, which corresponds to the ratio 40 : 25.
Therefore, the greatest ratio is 40 : 25.
Comparing this with the given options:
(A) 2 : 3
(B) 5 : 8
(C) 75 : 121
(D) 40 : 25
The correct option is (D) 40 : 25.
Question 9. There are ‘b’ boys and ‘g’ girls in a class. The ratio of the number of boys to the total number of students in the class is:
(A) $\frac{b}{b \;+ \;g}$
(B) $\frac{g}{b \;+ \;g}$
(C) $\frac{b}{g}$
(D) $\frac{b \;+ \;g}{b}$
Answer:
We are given the number of boys and girls in a class and need to find the ratio of the number of boys to the total number of students.
Number of boys = $b$
Number of girls = $g$
The total number of students in the class is the sum of the number of boys and the number of girls.
Total number of students = Number of boys + Number of girls = $b + g$.
The ratio of the number of boys to the total number of students is given by:
Ratio $= \frac{\text{Number of boys}}{\text{Total number of students}}$
Ratio $= \frac{b}{b + g}$
Comparing this expression with the given options:
(A) $\frac{b}{b \;+ \;g}$
(B) $\frac{g}{b \;+ \;g}$
(C) $\frac{b}{g}$
(D) $\frac{b \;+ \;g}{b}$
The expression $\frac{b}{b + g}$ matches option (A).
The correct option is (A) $\frac{b}{b \;+ \;g}$.
Question 10. If a bus travels 160 km in 4 hours and a train travels 320km in 5 hours at uniform speeds, then the ratio of the distances travelled by them in one hour is
(A) 1 : 2
(B) 4 : 5
(C) 5 : 8
(D) 8 : 5
Answer:
We need to find the ratio of the distances travelled by the bus and the train in one hour. This is equivalent to finding the ratio of their speeds, since speed is distance travelled per unit time.
Calculate the distance travelled by the bus in one hour (its speed):
Distance by bus = 160 km
Time taken by bus = 4 hours
Speed of bus = $\frac{\text{Distance}}{\text{Time}} = \frac{160 \text{ km}}{4 \text{ hours}}$
Speed of bus $= \frac{160}{4} \text{ km/hour} = 40 \text{ km/hour}$.
So, the bus travels 40 km in one hour.
Calculate the distance travelled by the train in one hour (its speed):
Distance by train = 320 km
Time taken by train = 5 hours
Speed of train = $\frac{\text{Distance}}{\text{Time}} = \frac{320 \text{ km}}{5 \text{ hours}}$
Speed of train $= \frac{320}{5} \text{ km/hour}$.
$320 \div 5 = 64$
Speed of train $= 64 \text{ km/hour}$.
So, the train travels 64 km in one hour.
Now, find the ratio of the distance travelled by the bus in one hour to the distance travelled by the train in one hour (ratio of their speeds):
Ratio $= \frac{\text{Distance by bus in 1 hour}}{\text{Distance by train in 1 hour}} = \frac{40 \text{ km}}{64 \text{ km}}$
Ratio $= \frac{40}{64}$
Simplify the fraction by dividing the numerator and the denominator by their greatest common divisor. Both are divisible by 8.
Ratio $= \frac{40 \div 8}{64 \div 8} = \frac{5}{8}$
The ratio is 5 : 8.
Comparing this with the given options:
(A) 1 : 2
(B) 4 : 5
(C) 5 : 8
(D) 8 : 5
The correct option is (C) 5 : 8.
Question 11 to 15 (Fill the Missing Number)
In questions 11 to 15, find the missing number in the box ⬜ in each of the proportions:
Question 11. $\frac{3}{5} = \frac{⬜}{20}$
Answer:
We are given a proportion with a missing number. We can solve for the missing number using equivalent fractions or cross-multiplication.
The given proportion is $\frac{3}{5} = \frac{⬜}{20}$.
Let the missing number be $x$. So, $\frac{3}{5} = \frac{x}{20}$.
Method 1: Equivalent Fractions
We observe the relationship between the denominators. To get from 5 to 20, we multiply by 4 ($5 \times 4 = 20$).
To maintain the equality of the fraction, we must perform the same operation on the numerator.
So, the missing numerator should be $3 \times 4$.
$x = 3 \times 4 = 12$.
Thus, $\frac{3}{5} = \frac{12}{20}$.
Method 2: Cross-Multiplication
In a proportion, the product of the means equals the product of the extremes.
$\frac{3}{5} = \frac{x}{20}$
$3 \times 20 = 5 \times x$
$60 = 5x$
To solve for $x$, divide both sides by 5:
$x = \frac{60}{5}$
$x = 12$.
The missing number in the box is 12.
Question 12. $\frac{⬜}{18} = \frac{2}{9}$
Answer:
We are given a proportion with a missing number. We can solve for the missing number using equivalent fractions or cross-multiplication.
The given proportion is $\frac{⬜}{18} = \frac{2}{9}$.
Let the missing number be $x$. So, $\frac{x}{18} = \frac{2}{9}$.
Method 1: Equivalent Fractions
We observe the relationship between the denominators. To get from 9 to 18, we multiply by 2 ($9 \times 2 = 18$).
To maintain the equality of the fraction, the numerator on the left must be the numerator on the right multiplied by the same factor (2).
So, the missing numerator should be $2 \times 2$.
$x = 2 \times 2 = 4$.
Thus, $\frac{4}{18} = \frac{2}{9}$.
Method 2: Cross-Multiplication
In a proportion, the product of the means equals the product of the extremes.
$\frac{x}{18} = \frac{2}{9}$
$x \times 9 = 18 \times 2$
$9x = 36$
To solve for $x$, divide both sides by 9:
$x = \frac{36}{9}$
$x = 4$.
The missing number in the box is 4.
Question 13. $\frac{8}{⬜} = \frac{3.2}{4}$
Answer:
We are given a proportion with a missing number. We can solve for the missing number using equivalent fractions or cross-multiplication.
The given proportion is $\frac{8}{⬜} = \frac{3.2}{4}$.
Let the missing number be $x$. So, $\frac{8}{x} = \frac{3.2}{4}$.
Method 1: Simplify the known ratio first
Simplify the ratio on the right side: $\frac{3.2}{4}$. We can multiply the numerator and denominator by 10 to remove the decimal.
$\frac{3.2}{4} = \frac{3.2 \times 10}{4 \times 10} = \frac{32}{40}$
Simplify the fraction $\frac{32}{40}$. Both are divisible by 8.
$\frac{32}{40} = \frac{32 \div 8}{40 \div 8} = \frac{4}{5}$
So, the proportion becomes $\frac{8}{x} = \frac{4}{5}$.
Now, observe the relationship between the numerators. To get from 4 to 8, we multiply by 2 ($4 \times 2 = 8$).
To maintain the equality, the denominator on the left must be the denominator on the right multiplied by the same factor (2).
So, the missing denominator should be $5 \times 2$.
$x = 5 \times 2 = 10$.
Thus, $\frac{8}{10} = \frac{4}{5} = \frac{3.2}{4}$.
Method 2: Cross-Multiplication
In a proportion, the product of the means equals the product of the extremes.
$\frac{8}{x} = \frac{3.2}{4}$
$8 \times 4 = x \times 3.2$
$32 = 3.2x$
To solve for $x$, divide both sides by 3.2:
$x = \frac{32}{3.2}$
Multiply the numerator and denominator by 10 to remove the decimal:
$x = \frac{32 \times 10}{3.2 \times 10} = \frac{320}{32}$
$x = 10$.
The missing number in the box is 10.
Question 14. $\frac{⬜}{45} = \frac{16}{40} = \frac{24}{⬜}$
Answer:
We are given a proportion with two missing numbers. This means the ratios are equal.
Let the two missing numbers, represented by the box symbol (⬜), be $x$ and $y$. Since they are in different positions in the proportion, they will likely have different values.
The given proportion is $\frac{x}{45} = \frac{16}{40} = \frac{24}{y}$.
First, let's simplify the known ratio $\frac{16}{40}$. Both numerator and denominator are divisible by 8.
$\frac{16}{40} = \frac{16 \div 8}{40 \div 8} = \frac{2}{5}$
So, the proportion can be written as $\frac{x}{45} = \frac{2}{5} = \frac{24}{y}$.
Now we can find the missing numbers by setting up equalities involving the known ratio $\frac{2}{5}$.
Finding the first missing number (x):
We use the equality $\frac{x}{45} = \frac{2}{5}$.
Using cross-multiplication:
$x \times 5 = 45 \times 2$
$5x = 90$
Divide both sides by 5:
$x = \frac{90}{5}$
$x = 18$
Finding the second missing number (y):
We use the equality $\frac{2}{5} = \frac{24}{y}$.
Using cross-multiplication:
$2 \times y = 5 \times 24$
$2y = 120$
Divide both sides by 2:
$y = \frac{120}{2}$
$y = 60$
The two missing numbers are 18 and 60.
The first missing number (in the numerator of the first ratio) is 18.
The second missing number (in the denominator of the third ratio) is 60.
Question 15. $\frac{16}{36} = \frac{⬜}{63} = \frac{36}{⬜} = \frac{⬜}{117}$
Answer:
We are given a series of equal ratios, which forms a proportion. There are three missing numbers, indicated by the box symbol (⬜).
The given proportion is $\frac{16}{36} = \frac{\Box_1}{63} = \frac{36}{\Box_2} = \frac{\Box_3}{117}$.
First, let's simplify the known ratio $\frac{16}{36}$ to its lowest terms.
Divide the numerator and the denominator by their greatest common divisor, which is 4.
$\frac{16}{36} = \frac{16 \div 4}{36 \div 4} = \frac{4}{9}$
So, the common ratio for all parts of the proportion is $\frac{4}{9}$.
Now, we find each missing number by setting the corresponding ratio equal to $\frac{4}{9}$.
Finding the first missing number ($\Box_1$):
We have $\frac{\Box_1}{63} = \frac{4}{9}$. Let $\Box_1 = x$.
$\frac{x}{63} = \frac{4}{9}$
Multiply both sides by 63:
$x = \frac{4}{9} \times 63$
$x = \frac{4 \times 63}{9}$
Cancel out the common factor 9:
$x = 4 \times \frac{\cancel{63}^{7}}{\cancel{9}_{1}}$
$x = 4 \times 7 = 28$
The first missing number is 28.
Finding the second missing number ($\Box_2$):
We have $\frac{36}{\Box_2} = \frac{4}{9}$. Let $\Box_2 = y$.
$\frac{36}{y} = \frac{4}{9}$
Using cross-multiplication:
$36 \times 9 = y \times 4$
$324 = 4y$
Divide both sides by 4:
$y = \frac{324}{4}$
$y = 81$
The second missing number is 81.
Finding the third missing number ($\Box_3$):
We have $\frac{\Box_3}{117} = \frac{4}{9}$. Let $\Box_3 = z$.
$\frac{z}{117} = \frac{4}{9}$
Multiply both sides by 117:
$z = \frac{4}{9} \times 117$
$z = \frac{4 \times 117}{9}$
Cancel out the common factor 9:
$z = 4 \times \frac{\cancel{117}^{13}}{\cancel{9}_{1}}$
$z = 4 \times 13 = 52$
The third missing number is 52.
The complete proportion with the missing numbers filled in is:
$\frac{16}{36} = \frac{28}{63} = \frac{36}{81} = \frac{52}{117}$
The missing numbers are 28, 81, and 52 in order of their appearance in the question.
Question 16 to 34 (True or False)
In questions 16 to 34, state whether the given statements are true (T) or false (F).
Question 16. $\frac{3}{8} = \frac{15}{40}$
Answer:
We need to check if the given equation is true.
The statement is $\frac{3}{8} = \frac{15}{40}$.
We can check this by simplifying the fraction on the right side or by using cross-multiplication.
Method 1: Simplify the right side
Consider the fraction $\frac{15}{40}$. We can divide the numerator and denominator by their greatest common divisor, which is 5.
$\frac{15}{40} = \frac{15 \div 5}{40 \div 5} = \frac{3}{8}$
Since $\frac{3}{8} = \frac{3}{8}$, the statement is true.
Method 2: Cross-multiplication
If the equation $\frac{3}{8} = \frac{15}{40}$ is true, then the cross-products must be equal.
$3 \times 40 = 8 \times 15$
$3 \times 40 = 120$
$8 \times 15 = 120$
Since $120 = 120$, the statement is true.
The statement is True (T).
Question 17. 4 : 7 = 20 : 35
Answer:
We need to state whether the given statement is true or false.
The statement is 4 : 7 = 20 : 35.
This can be written as an equality of fractions: $\frac{4}{7} = \frac{20}{35}$.
We can check this by simplifying the fraction on the right side or by using cross-multiplication.
Method 1: Simplify the right side
Consider the fraction $\frac{20}{35}$. We can divide the numerator and denominator by their greatest common divisor, which is 5.
$\frac{20}{35} = \frac{20 \div 5}{35 \div 5} = \frac{4}{7}$
Since $\frac{4}{7} = \frac{4}{7}$, the statement is true.
Method 2: Cross-multiplication
If the statement is true, the product of the extremes must equal the product of the means.
Extremes are 4 and 35. Means are 7 and 20.
$4 \times 35 = 140$
$7 \times 20 = 140$
Since $140 = 140$, the statement is true.
The statement is True (T).
Question 18. 0.2 : 5 = 2 : 0.5
Answer:
We need to state whether the given statement is true or false.
The statement is 0.2 : 5 = 2 : 0.5.
This can be written as an equality of fractions: $\frac{0.2}{5} = \frac{2}{0.5}$.
We can check this by simplifying both fractions or by using cross-multiplication.
Method 1: Simplify both sides
Left side: $\frac{0.2}{5}$. Multiply numerator and denominator by 10 to remove the decimal.
$\frac{0.2 \times 10}{5 \times 10} = \frac{2}{50}$
Simplify $\frac{2}{50}$ by dividing by 2:
$\frac{2 \div 2}{50 \div 2} = \frac{1}{25}$.
Right side: $\frac{2}{0.5}$. Multiply numerator and denominator by 10 to remove the decimal.
$\frac{2 \times 10}{0.5 \times 10} = \frac{20}{5}$
Simplify $\frac{20}{5}$:
$\frac{20}{5} = 4$.
Since $\frac{1}{25} \neq 4$, the statement is false.
Method 2: Cross-multiplication
If the statement is true, the product of the extremes must equal the product of the means.
Extremes are 0.2 and 0.5. Means are 5 and 2.
Product of extremes = $0.2 \times 0.5$
$0.2 \times 0.5 = 0.10 = 0.1$
Product of means = $5 \times 2 = 10$
Since $0.1 \neq 10$, the statement is false.
The statement is False (F).
Question 19. 3 : 33 = 33 : 333
Answer:
We need to state whether the given statement is true or false.
The statement is 3 : 33 = 33 : 333.
This can be written as an equality of fractions: $\frac{3}{33} = \frac{33}{333}$.
We can check this by simplifying both fractions or by using cross-multiplication.
Method 1: Simplify both sides
Left side: $\frac{3}{33}$. Divide both by 3.
$\frac{3 \div 3}{33 \div 3} = \frac{1}{11}$.
Right side: $\frac{33}{333}$. Both are divisible by 3.
$\frac{33 \div 3}{333 \div 3} = \frac{11}{111}$.
We need to check if $\frac{1}{11} = \frac{11}{111}$.
To compare these, we can find a common denominator or cross-multiply.
Cross-multiply: $1 \times 111$ vs $11 \times 11$.
$1 \times 111 = 111$
$11 \times 11 = 121$
Since $111 \neq 121$, the fractions are not equal, and the statement is false.
Method 2: Cross-multiplication directly
If the statement is true, the product of the extremes must equal the product of the means.
Extremes are 3 and 333. Means are 33 and 33.
Product of extremes = $3 \times 333$
$3 \times 333 = 999$.
Product of means = $33 \times 33$
$33 \times 33 = 1089$.
Since $999 \neq 1089$, the statement is false.
The statement is False (F).
Question 20. 15m : 40m = 35m : 65m
Answer:
We need to state whether the given statement is true or false.
The statement is 15m : 40m = 35m : 65m.
The units ('m') cancel out in each ratio, so we are checking if $\frac{15}{40} = \frac{35}{65}$.
We can check this by simplifying both fractions or by using cross-multiplication.
Method 1: Simplify both sides
Left side: $\frac{15}{40}$. Divide both by 5.
$\frac{15 \div 5}{40 \div 5} = \frac{3}{8}$.
Right side: $\frac{35}{65}$. Both are divisible by 5.
$\frac{35 \div 5}{65 \div 5} = \frac{7}{13}$.
We need to check if $\frac{3}{8} = \frac{7}{13}$.
To compare these, we can cross-multiply.
$3 \times 13$ vs $8 \times 7$.
$3 \times 13 = 39$
$8 \times 7 = 56$
Since $39 \neq 56$, the fractions are not equal, and the statement is false.
Method 2: Cross-multiplication directly
If the statement is true, the product of the extremes must equal the product of the means.
Extremes are 15m and 65m. Means are 40m and 35m.
Product of extremes = $15 \times 65$
$\begin{array}{cc}& & 1 & 5 \\ \times & & 6 & 5 \\ \hline & & 7 & 5 \\ 9 & 0 & \times \\ \hline 9 & 7 & 5 \\ \hline \end{array}$
Product of extremes = 975.
Product of means = $40 \times 35$
$40 \times 35 = 4 \times 10 \times 35 = 4 \times 350 = 1400$.
Since $975 \neq 1400$, the statement is false.
The statement is False (F).
Question 21. 27cm2 : 57cm2 = 18cm : 38cm
Answer:
We need to state whether the given statement is true or false.
The statement is 27cm$^2$ : 57cm$^2$ = 18cm : 38cm.
The units cancel out in each ratio, so we are checking if $\frac{27}{57} = \frac{18}{38}$.
We can check this by simplifying both fractions or by using cross-multiplication.
Method 1: Simplify both sides
Left side: $\frac{27}{57}$. Both are divisible by 3.
$\frac{27 \div 3}{57 \div 3} = \frac{9}{19}$.
Right side: $\frac{18}{38}$. Both are divisible by 2.
$\frac{18 \div 2}{38 \div 2} = \frac{9}{19}$.
Since $\frac{9}{19} = \frac{9}{19}$, the fractions are equal, and the statement is true.
Method 2: Cross-multiplication directly
If the statement is true, the product of the extremes must equal the product of the means.
Extremes are 27 and 38. Means are 57 and 18.
Product of extremes = $27 \times 38$
$\begin{array}{cc}& & 2 & 7 \\ \times & & 3 & 8 \\ \hline & 2 & 1 & 6 \\ 8 & 1 & \times \\ \hline 10 & 2 & 6 \\ \hline \end{array}$
Product of extremes = 1026.
Product of means = $57 \times 18$
$\begin{array}{cc}& & 5 & 7 \\ \times & & 1 & 8 \\ \hline & 4 & 5 & 6 \\ 5 & 7 & \times \\ \hline 10 & 2 & 6 \\ \hline \end{array}$
Product of means = 1026.
Since $1026 = 1026$, the statement is true.
The statement is True (T).
Question 22. 5kg : 7.5kg = Rs 7.50 : Rs 5
Answer:
We need to state whether the given statement is true or false.
The statement is 5kg : 7.5kg = $\textsf{₹}$ 7.50 : $\textsf{₹}$ 5.
The units cancel out in each ratio, so we are checking if $\frac{5}{7.5} = \frac{7.5}{5}$.
We can check this by simplifying both sides or by using cross-multiplication.
Method 1: Simplify both sides
Left side: $\frac{5}{7.5}$. Multiply numerator and denominator by 10 to remove the decimal.
$\frac{5 \times 10}{7.5 \times 10} = \frac{50}{75}$
Simplify $\frac{50}{75}$ by dividing both by 25.
$\frac{50 \div 25}{75 \div 25} = \frac{2}{3}$.
Right side: $\frac{7.5}{5}$. Multiply numerator and denominator by 10 to remove the decimal.
$\frac{7.5 \times 10}{5 \times 10} = \frac{75}{50}$
Simplify $\frac{75}{50}$ by dividing both by 25.
$\frac{75 \div 25}{50 \div 25} = \frac{3}{2}$.
We need to check if $\frac{2}{3} = \frac{3}{2}$.
Since $\frac{2}{3} \neq \frac{3}{2}$, the statement is false.
Method 2: Cross-multiplication directly
If the statement is true, the product of the extremes must equal the product of the means.
Extremes are 5kg and $\textsf{₹}$ 5. Means are 7.5kg and $\textsf{₹}$ 7.50.
Product of extremes = $5 \times 5 = 25$.
Product of means = $7.5 \times 7.5$
$7.5 \times 7.5 = (7.5)^2$
$75 \times 75 = 5625$. With two decimal places, $7.5 \times 7.5 = 56.25$.
Product of means = 56.25.
Since $25 \neq 56.25$, the statement is false.
The statement is False (F).
Question 23. 20g : 100g = 1metre : 500cm
Answer:
We need to state whether the given statement is true or false.
The statement is 20g : 100g = 1metre : 500cm.
For the ratios to be equal, the quantities within each ratio must be in the same unit (which they are on the left side, 'g') or convertible to the same unit (which is the case on the right side, 'metre' and 'cm'). The units cancel out when forming the ratio.
Left side ratio: 20g : 100g = $\frac{20}{100}$.
Simplify the fraction by dividing both by 20.
$\frac{20 \div 20}{100 \div 20} = \frac{1}{5}$.
Right side ratio: 1 metre : 500 cm.
Convert units to be the same. We know that 1 metre = 100 cm.
The ratio is 100 cm : 500 cm = $\frac{100}{500}$.
Simplify the fraction by dividing both by 100.
$\frac{100 \div 100}{500 \div 100} = \frac{1}{5}$.
We are checking if $\frac{1}{5} = \frac{1}{5}$.
Since $\frac{1}{5} = \frac{1}{5}$, the statement is true.
The statement is True (T).
Question 24. 12 hours : 30 hours = 8km : 20km
Answer:
We need to state whether the given statement is true or false.
The statement is 12 hours : 30 hours = 8km : 20km.
The units ('hours' and 'km') cancel out in each ratio, so we are checking if $\frac{12}{30} = \frac{8}{20}$.
We can check this by simplifying both fractions or by using cross-multiplication.
Method 1: Simplify both sides
Left side: $\frac{12}{30}$. Divide both by their GCD, which is 6.
$\frac{12 \div 6}{30 \div 6} = \frac{2}{5}$.
Right side: $\frac{8}{20}$. Divide both by their GCD, which is 4.
$\frac{8 \div 4}{20 \div 4} = \frac{2}{5}$.
We need to check if $\frac{2}{5} = \frac{2}{5}$.
Since $\frac{2}{5} = \frac{2}{5}$, the statement is true.
Method 2: Cross-multiplication directly
If the statement is true, the product of the extremes must equal the product of the means.
Extremes are 12 hours and 20km. Means are 30 hours and 8km.
$12 \times 20 = 240$
$30 \times 8 = 240$
Since $240 = 240$, the statement is true.
The statement is True (T).
Question 25. The ratio of 10kg to 100kg is 1:10
Answer:
We need to determine if the ratio of 10kg to 100kg is 1:10.
Ratio $= \frac{\text{Quantity 1}}{\text{Quantity 2}} = \frac{10 \text{ kg}}{100 \text{ kg}}$
The units ('kg') cancel out.
Ratio $= \frac{10}{100}$
Simplify the fraction by dividing the numerator and the denominator by their greatest common divisor, which is 10.
Ratio $= \frac{10 \div 10}{100 \div 10} = \frac{1}{10}$
The ratio is 1 : 10.
The statement says the ratio is 1:10, which matches our calculated ratio.
The statement is True (T).
Question 26. The ratio of 150cm to 1metre is 1:1.5.
Answer:
We need to determine if the ratio of 150cm to 1metre is 1:1.5.
To find the ratio, the quantities must be in the same unit.
Convert 1 metre to centimeters. We know that 1 metre = 100 cm.
The quantities are 150 cm and 100 cm.
Ratio $= \frac{\text{Quantity 1}}{\text{Quantity 2}} = \frac{150 \text{ cm}}{100 \text{ cm}}$
The units cancel out.
Ratio $= \frac{150}{100}$
Simplify the fraction by dividing the numerator and the denominator by their greatest common divisor, which is 50.
Ratio $= \frac{150 \div 50}{100 \div 50} = \frac{3}{2}$
The ratio is 3 : 2.
The statement says the ratio is 1:1.5. Let's convert 1:1.5 to a fraction:
$1 : 1.5 = \frac{1}{1.5} = \frac{1 \times 10}{1.5 \times 10} = \frac{10}{15}$.
Simplify $\frac{10}{15}$ by dividing both by 5.
$\frac{10 \div 5}{15 \div 5} = \frac{2}{3}$.
The stated ratio is equivalent to 2:3.
We found the ratio to be 3:2, but the statement claims it is 1:1.5 (which is 2:3).
Since $3:2 \neq 2:3$, the statement is false.
The statement is False (F).
Question 28. The ratio of 1 hour to one day is 1:1.
Answer:
We need to determine if the ratio of 1 hour to one day is 1:1.
To find the ratio, the quantities must be in the same unit.
Convert one day to hours. We know that 1 day = 24 hours.
The quantities are 1 hour and 24 hours.
Ratio $= \frac{\text{Quantity 1}}{\text{Quantity 2}} = \frac{1 \text{ hour}}{24 \text{ hours}}$
The units ('hours') cancel out.
Ratio $= \frac{1}{24}$
The ratio is 1 : 24.
The statement says the ratio is 1:1. We found the ratio to be 1:24.
Since $1:24 \neq 1:1$, the statement is false.
The statement is False (F).
Question 29. The ratio 4:16 is in its lowest form.
Answer:
A ratio is in its lowest form if the greatest common divisor (GCD) of its two terms is 1.
The given ratio is 4 : 16, which can be written as the fraction $\frac{4}{16}$.
To find if it's in lowest form, we find the GCD of 4 and 16.
The divisors of 4 are 1, 2, 4.
The divisors of 16 are 1, 2, 4, 8, 16.
The common divisors are 1, 2, 4.
The greatest common divisor (GCD) of 4 and 16 is 4.
Since the GCD is 4 (and not 1), the ratio is not in its lowest form.
To write it in lowest form, divide both terms by the GCD:
$4 \div 4 = 1$
$16 \div 4 = 4$
The lowest form of the ratio 4:16 is 1:4.
The statement says that the ratio 4:16 is in its lowest form, which is incorrect.
The statement is False (F).
Question 30. The ratio 5 : 4 is different from the ratio 4 : 5.
Answer:
A ratio compares two quantities in a specific order. The order matters.
The ratio 5 : 4 can be written as the fraction $\frac{5}{4}$.
This means Quantity 1 is 5 units for every 4 units of Quantity 2.
The ratio 4 : 5 can be written as the fraction $\frac{4}{5}$.
This means Quantity 1 is 4 units for every 5 units of Quantity 2.
Comparing the fractions $\frac{5}{4}$ and $\frac{4}{5}$:
$\frac{5}{4} = 1.25$
$\frac{4}{5} = 0.8$
Since $1.25 \neq 0.8$, the fractions are not equal.
Therefore, the ratio 5 : 4 is different from the ratio 4 : 5.
The statement is True (T).
Question 31. A ratio will always be more than 1.
Answer:
We need to determine if a ratio will always be more than 1.
A ratio compares two quantities. If the first quantity is greater than the second quantity, the ratio will be greater than 1. If the first quantity is less than the second quantity, the ratio will be less than 1.
Consider some examples:
- The ratio of 5 to 2 is $\frac{5}{2} = 2.5$, which is more than 1.
- The ratio of 2 to 5 is $\frac{2}{5} = 0.4$, which is less than 1.
- The ratio of 3 to 3 is $\frac{3}{3} = 1$, which is equal to 1.
Since we can have ratios that are less than 1 (like 2:5 or $\frac{2}{5}$) or equal to 1 (like 3:3 or $\frac{3}{3}$), the statement that a ratio will always be more than 1 is incorrect.
The statement is False (F).
Question 32. A ratio can be equal to 1.
Answer:
We need to determine if a ratio can be equal to 1.
A ratio of two quantities $\frac{a}{b}$ is equal to 1 if the numerator and the denominator are equal, provided the denominator is not zero.
Consider the ratio of a quantity to itself, for example, the ratio of 5 cm to 5 cm.
Ratio $= \frac{5 \text{ cm}}{5 \text{ cm}} = \frac{5}{5} = 1$.
Consider the ratio of any non-zero number to itself, say $k$, where $k \neq 0$.
Ratio $= \frac{k}{k} = 1$.
Since we can find instances where a ratio is equal to 1 (when the two quantities being compared are equal), the statement is true.
The statement is True (T).
Question 33. If b : a = c : d, then a, b, c, d are in proportion.
Answer:
A proportion is a statement of equality between two ratios. If four quantities $p, q, r, s$ are in proportion, it means that the ratio of the first to the second is equal to the ratio of the third to the fourth, i.e., $p : q = r : s$, or $\frac{p}{q} = \frac{r}{s}$. In this case, $p, q, r, s$ are said to be in proportion in that order.
The given statement is "If $b : a = c : d$, then $a, b, c, d$ are in proportion."
The equation $b : a = c : d$ means $\frac{b}{a} = \frac{c}{d}$.
For the quantities $a, b, c, d$ to be in proportion in that order, the ratio of the first to the second must equal the ratio of the third to the fourth, i.e., $a : b = c : d$, or $\frac{a}{b} = \frac{c}{d}$.
We are given $\frac{b}{a} = \frac{c}{d}$ and we need to check if this implies $\frac{a}{b} = \frac{c}{d}$.
Consider the given equation $\frac{b}{a} = \frac{c}{d}$. Taking the reciprocal of both sides (assuming $a, b, c, d$ are non-zero):
$\frac{1}{(\frac{b}{a})} = \frac{1}{(\frac{c}{d})}$
$\frac{a}{b} = \frac{d}{c}$
This shows that if $b : a = c : d$, then $a : b = d : c$, not necessarily $a : b = c : d$.
Let's take a numerical example.
Let $b = 2, a = 1, c = 4, d = 2$.
Check if $b : a = c : d$ is true:
$2 : 1 = \frac{2}{1} = 2$
$4 : 2 = \frac{4}{2} = 2$
So, $2 : 1 = 4 : 2$ is true. This means $\frac{b}{a} = \frac{c}{d}$ is satisfied with $b=2, a=1, c=4, d=2$.
Now check if $a, b, c, d$ are in proportion, i.e., $a : b = c : d$.
$1 : 2 = \frac{1}{2}$
$4 : 2 = \frac{4}{2} = 2$
Since $\frac{1}{2} \neq 2$, $a, b, c, d$ are not in proportion.
The statement is False (F).
Question 34. The two terms of a ratio can be in two different units.
Answer:
A ratio is a comparison of two quantities. For a ratio to be meaningful, the quantities being compared must be of the same kind or have the same unit.
For example, we can compare 5 kg to 10 kg, and the ratio is $5:10 = 1:2$. The unit 'kg' cancels out.
We can compare 1 hour to 30 minutes. We first convert them to the same unit (e.g., minutes). 1 hour = 60 minutes. The ratio is 60 minutes : 30 minutes = $60:30 = 2:1$. The unit 'minutes' cancels out.
If the two terms of a ratio are in fundamentally different units that cannot be converted to each other (like length and mass, or time and volume), then the ratio does not represent a simple comparison of magnitude, although sometimes rates (which are ratios of quantities with different units) are encountered in mathematics and science (e.g., km/hour, density = mass/volume). However, a standard ratio as defined usually requires the quantities to be of the same kind for direct comparison.
In the context of ratios as taught in introductory levels, the quantities being compared typically need to be in the same units so that the ratio is a dimensionless number.
Consider the wording "The two terms of a ratio can be in two different units." This phrasing can be interpreted in two ways:
1. Can the units be different initially but convertible? Yes (e.g., cm and m).
2. Can the units be different and not convertible (e.g., kg and metres)? In the context of a simple ratio comparing magnitudes of the same kind of quantity, no. In the context of rates, yes, but the question asks about a "ratio".
Given the level of the questions (Class 6 NCERT Exemplar), the intended meaning is likely that the quantities should be of the same type, allowing for comparison once units are made consistent. The statement "can be in two different units" might imply non-convertible units, in which case the standard ratio definition doesn't apply directly for simple comparison.
However, if the question means "can the units be different initially, requiring conversion?", then the answer would be True. But the phrasing "two different units" is slightly ambiguous.
Considering common definitions of ratios, the terms should represent quantities of the same kind. If they are of the same kind but in different units (like metres and centimetres), you convert to the same unit before finding the ratio.
If the units are fundamentally different (like meters and kilograms), they cannot form a standard ratio in the way usually taught. They form a rate.
The statement as written "can be in two different units" is most likely intended to mean units that are fundamentally different and not inter-convertible for direct comparison of magnitude.
Therefore, based on the standard definition of a ratio for comparing magnitudes of the same type of quantity, the statement is False.
The statement is False (F).
Question 35 to 46 (Fill in the Blanks)
In questions 35 to 46, fill in the blanks to make the statements true.
Question 35. A ratio is a form of comparison by ______.
Answer:
A ratio is a form of comparison by division.
A ratio is a way to compare two quantities of the same kind. It expresses how many times one quantity is contained in the other or what fraction one quantity is of the other.
This comparison is done using the operation of division. When we write a ratio $a:b$, it means we are comparing the quantity $a$ to the quantity $b$ by considering the quotient $\frac{a}{b}$. The ratio $a:b$ is numerically equal to the value of the fraction $\frac{a}{b}$.
For example, if you have 6 apples and 3 oranges, the ratio of apples to oranges can be written as $6:3$. This ratio is equivalent to the fraction $\frac{6}{3}$, which simplifies to 2. This means the number of apples is 2 times the number of oranges, illustrating a comparison by division.
Question 36. 20m : 70m = Rs 8 : Rs ______.
Answer:
The given relation is a proportion. A proportion states that two ratios are equal.
Let the missing value be $x$. The proportion can be written as:
$\frac{20 \text{ m}}{70 \text{ m}} = \frac{\text{Rs } 8}{\text{Rs } x}$
... (i)
The units in the ratio on the left side cancel out, and similarly, the units in the ratio on the right side will cancel out when we solve for $x$. We can write the equation as:
$\frac{20}{70} = \frac{8}{x}$
Simplify the fraction on the left side:
$\frac{\cancel{20}^{2}}{\cancel{70}^{7}} = \frac{2}{7}$
So the equation becomes:
$\frac{2}{7} = \frac{8}{x}$
To solve for $x$, we can cross-multiply:
$2 \times x = 7 \times 8$
$2x = 56$
Now, divide both sides by 2:
$x = \frac{56}{2}$
$x = 28$
Thus, the missing value is 28. The proportion is 20m : 70m = Rs 8 : Rs 28.
The final answer is 28.
Question 37. There is a number in the box ⬜ such that ⬜ , 24, 9, 12 are in proportion. The number in the box is _____.
Answer:
If four quantities are in proportion, the ratio of the first to the second is equal to the ratio of the third to the fourth.
Let the number in the box be $y$. The given proportion is:
$y : 24 :: 9 : 12$
This can be written as an equation of ratios:
$\frac{y}{24} = \frac{9}{12}$
... (i)
Simplify the ratio on the right side:
$\frac{9}{12} = \frac{\cancel{9}^{3}}{\cancel{12}^{4}} = \frac{3}{4}$
The equation becomes:
$\frac{y}{24} = \frac{3}{4}$
To solve for $y$, multiply both sides of the equation by 24:
$y = \frac{3}{4} \times 24$
$y = 3 \times \frac{24}{4}$
$y = 3 \times \cancel{6}$
$y = 18$
Thus, the number in the box is 18.
The final answer is 18.
Question 38. If two ratios are equal, then they are in _____.
Answer:
If two ratios are equal, then they are in proportion.
A proportion is a statement that two ratios are equal. If we have two ratios, say $a:b$ and $c:d$, and they are equal, we write this as $a:b :: c:d$. This notation means that the ratio of $a$ to $b$ is equal to the ratio of $c$ to $d$.
In terms of fractions, this is expressed as $\frac{a}{b} = \frac{c}{d}$. The quantities $a, b, c,$ and $d$ are called the terms of the proportion. $a$ and $d$ are the extreme terms (or extremes), and $b$ and $c$ are the middle terms (or means).
A fundamental property of a proportion is that the product of the extremes is equal to the product of the means, i.e., $a \times d = b \times c$.
Use Fig. 8.2 (In which each square is of unit length) for questions 39 and 40:

Question 39. The ratio of the perimeter of the boundary of the shaded portion to the perimeter of the whole figure is _______.
Answer:
First, let's determine the dimensions of the whole figure from the grid. Each square is of unit length.
Counting the number of squares along the width (horizontal) of the whole figure, we find there are 5 squares.
Counting the number of squares along the height (vertical) of the whole figure, we find there are 4 squares.
So, the whole figure is a rectangle with width 5 units and height 4 units.
The perimeter of the whole figure is the total length of its boundary.
Perimeter of rectangle = $2 \times (\text{width} + \text{height})$
Perimeter of the whole figure = $2 \times (5 + 4) = 2 \times 9 = 18$ units.
Next, let's determine the perimeter of the boundary of the shaded portion. The boundary consists of all the unit-length segments that form the outline of the shaded area.
These segments are the edges of the shaded squares that are adjacent to either an unshaded square or the outside boundary of the whole figure.
Let's count the number of such segments:
Horizontal segments on the boundary:
- Top edge of the shaded area (Row 1, columns 1-3): 3 units
- Bottom edge of the shaded area (Row 4, columns 1-3): 3 units
- Horizontal edges between Row 1 and Row 2 (shaded vs empty): between (R1,C1)S and (R2,C1)E, between (R1,C2)S and (R2,C2)E. Total 2 units.
- Horizontal edges between Row 2 and Row 3: no S-E boundary (R2,C3 and R3,C3 are both S). Total 0 units.
- Horizontal edges between Row 3 and Row 4 (empty vs shaded): between (R3,C1)E and (R4,C1)S, between (R3,C2)E and (R4,C2)S. Total 2 units.
Total horizontal segments = $3 + 3 + 2 + 0 + 2 = 10$ units.
Vertical segments on the boundary:
- Left edge of the shaded area (along Column 1): left edge of (R1,C1)S, left edge of (R4,C1)S. Total 2 units. (The left edges of R2,C1 and R3,C1 are on the grid boundary but adjacent to empty cells).
- Right edge of the shaded area (along Column 3): right edge of (R1,C3)S, (R2,C3)S, (R3,C3)S, (R4,C3)S. Total 4 units. (These edges are adjacent to empty squares in Column 4).
- Vertical edges between Column 1 and Column 2: no S-E boundary. Total 0 units.
- Vertical edges between Column 2 and Column 3: between (R2,C2)E and (R2,C3)S, between (R3,C2)E and (R3,C3)S. Total 2 units.
- Vertical edges between Column 3 and Column 4: between (R1,C3)S and (R1,C4)E, between (R2,C3)S and (R2,C4)E, between (R3,C3)S and (R3,C4)E, between (R4,C3)S and (R4,C4)E. Total 4 units.
Total vertical segments = $2 + 4 + 0 + 2 + 4 = 12$ units.
The perimeter of the boundary of the shaded portion is the sum of all horizontal and vertical boundary segments.
Perimeter of shaded portion = Total horizontal segments + Total vertical segments = $10 + 12 = 22$ units.
The ratio of the perimeter of the boundary of the shaded portion to the perimeter of the whole figure is:
Ratio = $\frac{\text{Perimeter of shaded portion}}{\text{Perimeter of whole figure}} = \frac{22}{18}$
Simplify the ratio by dividing the numerator and denominator by their greatest common divisor, which is 2.
$\frac{\cancel{22}^{11}}{\cancel{18}_{9}} = \frac{11}{9}$
The ratio is 11:9.
The final answer is 11:9.
Question 40. The ratio of the area of the shaded portion to that of the whole figure is ______.
Answer:
The area of a figure made up of unit squares is equal to the number of unit squares it contains.
First, let's find the area of the whole figure. The whole figure is a rectangle formed by the grid.
The width of the whole figure is 5 units (5 squares horizontally).
The height of the whole figure is 4 units (4 squares vertically).
Area of the whole figure = Number of squares in the whole figure = Width $\times$ Height = $5 \times 4 = 20$ square units.
Next, let's find the area of the shaded portion by counting the number of shaded squares.
Counting the shaded squares:
- Top row: 3 shaded squares
- Second row: 1 shaded square
- Third row: 1 shaded square
- Bottom row: 3 shaded squares
Total number of shaded squares = $3 + 1 + 1 + 3 = 8$ squares.
Area of the shaded portion = 8 square units.
The ratio of the area of the shaded portion to that of the whole figure is given by:
Ratio = $\frac{\text{Area of shaded portion}}{\text{Area of whole figure}} = \frac{8}{20}$
To simplify the ratio $\frac{8}{20}$, we find the greatest common divisor (GCD) of 8 and 20, which is 4.
Divide both the numerator and the denominator by 4:
$\frac{\cancel{8}^{2}}{\cancel{20}_{5}} = \frac{2}{5}$
The ratio is 2:5.
The final answer is 2:5.
Question 41. Sleeping time of a python in a 24 hour clock is represented by the shaded portion in Fig. 8.3
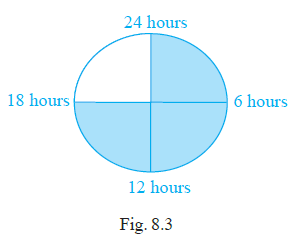
The ratio of sleeping time to awaking time is ______.
Answer:
The clock represents a 24-hour period.
The shaded portion in Fig. 8.3 shows the sleeping time of the python.
By counting the number of shaded hour segments on the clock, we can determine the sleeping time.
The shaded portion covers the hours from 12 to 18.
Sleeping time = $18 - 12 = 6$ hours.
The awaking time is the remaining part of the 24-hour day.
Total time = 24 hours.
Awaking time = Total time - Sleeping time
Awaking time = $24 - 6 = 18$ hours.
We need to find the ratio of sleeping time to awaking time.
Ratio = Sleeping time : Awaking time
Ratio = 6 hours : 18 hours
To simplify the ratio, we find the greatest common divisor (GCD) of 6 and 18, which is 6. We divide both parts of the ratio by 6.
Ratio = $\frac{6}{18} = \frac{\cancel{6}^{1}}{\cancel{18}_{3}} = \frac{1}{3}$
The ratio is 1:3.
The final answer is 1:3.
Question 42. A ratio expressed in lowest form has no common factor other than ______ in its terms.
Answer:
A ratio expressed in lowest form has no common factor other than 1 in its terms.
A ratio compares two quantities, say $a$ and $b$, often written as $a:b$ or $\frac{a}{b}$.
A ratio is said to be in its lowest form (or simplest form) when the two terms of the ratio (the numerator and the denominator when written as a fraction) have no common factor other than 1.
To express a ratio in its lowest form, we divide both terms by their greatest common divisor (GCD).
For example, consider the ratio $12:18$. The terms are 12 and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest common divisor is 6.
Dividing both terms by 6:
$\frac{12 \div 6}{18 \div 6} = \frac{2}{3}$
So, the ratio $12:18$ in lowest form is $2:3$. The terms 2 and 3 have no common factor other than 1.
Question 43. To find the ratio of two quantities, they must be expressed in _____units.
Answer:
To find the ratio of two quantities, they must be expressed in same units.
A ratio is a comparison of two quantities of the same kind. For the comparison to be valid and meaningful, both quantities must be measured in the same unit.
For example, to find the ratio of 50 cm to 2 meters, you cannot directly form the ratio $50:2$ because the units (cm and meters) are different.
You must convert one of the quantities so they share the same unit. For instance, convert meters to centimeters:
$2 \text{ meters} = 2 \times 100 \text{ cm} = 200 \text{ cm}$.
Now, both quantities are in centimeters: 50 cm and 200 cm. The ratio can be formed and simplified:
Ratio = $50 \text{ cm} : 200 \text{ cm}$
Ratio = $\frac{50}{200} = \frac{\cancel{50}^{1}}{\cancel{200}_{4}} = \frac{1}{4}$
The ratio is 1:4. Note that the units cancel out in the ratio.
If the units were different (e.g., ratio of length to mass), it would not be a standard ratio but a rate (like speed, which is distance/time). For a simple ratio, the units must be identical.
Question 44. Ratio of 5 paise to 25 paise is the same as the ratio of 20 paise to _____
Answer:
The problem states that two ratios are equal. Let the missing value be $x$ paise.
The first ratio is 5 paise : 25 paise.
The second ratio is 20 paise : $x$ paise.
Since the ratios are the same, we can set up a proportion:
$\frac{5 \text{ paise}}{25 \text{ paise}} = \frac{20 \text{ paise}}{x \text{ paise}}$
... (i)
The units cancel out in both ratios. We can write the equation as:
$\frac{5}{25} = \frac{20}{x}$
Simplify the fraction on the left side:
$\frac{\cancel{5}^{1}}{\cancel{25}_{5}} = \frac{1}{5}$
The equation becomes:
$\frac{1}{5} = \frac{20}{x}$
To solve for $x$, we cross-multiply:
$1 \times x = 5 \times 20$
$x = 100$
So, the missing value is 100 paise.
The final answer is 100 paise.
Question 45. Saturn and Jupiter take 9 hours 56 minutes and 10 hours 40 minutes, respectively for one spin on their axes. The ratio of the time taken by Saturn and Jupiter in lowest form is ______.
Answer:
To find the ratio of the time taken, the times must be in the same unit. We will convert both times to minutes.
1 hour = 60 minutes.
Time taken by Saturn = 9 hours 56 minutes
Time taken by Saturn = $(9 \times 60) \text{ minutes} + 56 \text{ minutes}$
Time taken by Saturn = $540 \text{ minutes} + 56 \text{ minutes}$
Time taken by Saturn = 596 minutes.
Time taken by Jupiter = 10 hours 40 minutes
Time taken by Jupiter = $(10 \times 60) \text{ minutes} + 40 \text{ minutes}$
Time taken by Jupiter = $600 \text{ minutes} + 40 \text{ minutes}$
Time taken by Jupiter = 640 minutes.
The ratio of the time taken by Saturn to the time taken by Jupiter is:
Ratio = $\frac{\text{Time taken by Saturn}}{\text{Time taken by Jupiter}} = \frac{596 \text{ minutes}}{640 \text{ minutes}}$
Ratio = $\frac{596}{640}$
Now, we simplify this fraction to its lowest form by dividing the numerator and denominator by their greatest common divisor (GCD).
We can divide both numbers by 2:
$\frac{596 \div 2}{640 \div 2} = \frac{298}{320}$
Again, divide both by 2:
$\frac{298 \div 2}{320 \div 2} = \frac{149}{160}$
Now, we check if 149 and 160 have any common factors other than 1. The number 149 is a prime number. Since 160 is not divisible by 149, the greatest common divisor of 149 and 160 is 1.
Therefore, the ratio $\frac{149}{160}$ is in its lowest form.
The ratio is 149:160.
The final answer is 149:160.
Question 46. 10g of caustic soda dissolved in 100mL of water makes a solution of caustic soda. Amount of caustic soda needed for 1 litre of water to make the same type of solution is ______.
Answer:
The problem states that we need to make the same type of solution, which means the concentration of caustic soda in water must be the same in both cases. Concentration can be expressed as the ratio of the amount of caustic soda to the amount of water.
In the first case, the ratio of caustic soda to water is 10 g : 100 mL.
In the second case, we have 1 litre of water. To maintain the same ratio, the amount of caustic soda must be in proportion to the amount of water. First, convert 1 litre to millilitres so the units are consistent:
$1 \text{ litre} = 1000 \text{ mL}$.
Let $x$ be the amount of caustic soda (in grams) needed for 1000 mL of water to make the same type of solution. The ratio in the second case is $x$ g : 1000 mL.
Since the ratios are equal, we can write a proportion:
$\frac{10 \text{ g}}{100 \text{ mL}} = \frac{x \text{ g}}{1000 \text{ mL}}$
... (i)
The units cancel out as they are the same in the numerator and denominator on each side. We can write the equation without units for calculation:
$\frac{10}{100} = \frac{x}{1000}$
Simplify the fraction on the left side:
$\frac{\cancel{10}^{1}}{\cancel{100}_{10}} = \frac{1}{10}$
The equation becomes:
$\frac{1}{10} = \frac{x}{1000}$
To solve for $x$, multiply both sides of the equation by 1000:
$x = \frac{1}{10} \times 1000$
$x = \frac{1000}{10}$
$x = 100$
So, 100 grams of caustic soda are needed for 1 litre (1000 mL) of water to make the same type of solution.
The final answer is 100 g.
Question 47 to 89
Question 47. The marked price of a table is Rs 625 and its sale price is Rs 500. What is the ratio of the sale price to the marked price?
Answer:
Given:
Marked Price = $\textsf{₹}$ 625
Sale Price = $\textsf{₹}$ 500
We need to find the ratio of the Sale Price to the Marked Price.
Ratio = Sale Price : Marked Price
Ratio = $\textsf{₹}$ 500 : $\textsf{₹}$ 625
We can write this as a fraction:
Ratio = $\frac{500}{625}$
To find the ratio in the lowest form, we simplify the fraction by dividing the numerator and denominator by their greatest common divisor (GCD).
Let's find the GCD of 500 and 625.
Both numbers are divisible by 25 (since they end in 00 and 25 respectively):
$\frac{500 \div 25}{625 \div 25} = \frac{20}{25}$
Now, both 20 and 25 are divisible by 5:
$\frac{20 \div 5}{25 \div 5} = \frac{4}{5}$
The numbers 4 and 5 have no common factor other than 1, so the fraction is in its lowest form.
The ratio of the sale price to the marked price is 4:5.
The final answer is 4:5.
Question 48. Which pair of ratios are equal? And why?
(i) $\frac{2}{3}$ , $\frac{4}{6}$
(ii) $\frac{8}{4}$ , $\frac{2}{1}$
(iii) $\frac{4}{5}$ , $\frac{12}{20}$
Answer:
To check if two ratios are equal, we can simplify them to their lowest forms or check if their cross-products are equal.
(i) $\frac{2}{3}$ , $\frac{4}{6}$
The first ratio is already in its lowest form: $\frac{2}{3}$.
Simplify the second ratio $\frac{4}{6}$ by dividing the numerator and denominator by their GCD, which is 2:
$\frac{4}{6} = \frac{\cancel{4}^{2}}{\cancel{6}_{3}} = \frac{2}{3}$
Since $\frac{2}{3} = \frac{2}{3}$, the ratios are equal.
(ii) $\frac{8}{4}$ , $\frac{2}{1}$
Simplify the first ratio $\frac{8}{4}$ by dividing the numerator and denominator by their GCD, which is 4:
$\frac{8}{4} = \frac{\cancel{8}^{2}}{\cancel{4}_{1}} = \frac{2}{1}$
The second ratio is already in its lowest form: $\frac{2}{1}$.
Since $\frac{2}{1} = \frac{2}{1}$, the ratios are equal.
(iii) $\frac{4}{5}$ , $\frac{12}{20}$
The first ratio is already in its lowest form: $\frac{4}{5}$.
Simplify the second ratio $\frac{12}{20}$ by dividing the numerator and denominator by their GCD, which is 4:
$\frac{12}{20} = \frac{\cancel{12}^{3}}{\cancel{20}_{5}} = \frac{3}{5}$
Since $\frac{4}{5} \neq \frac{3}{5}$, the ratios are not equal.
Therefore, the pairs of equal ratios are (i) and (ii).
Question 49. Which ratio is larger 10 : 21 or 21 : 93?
Answer:
To compare the two ratios, we can express them as fractions and then compare the fractions.
The first ratio is $10 : 21$, which can be written as the fraction $\frac{10}{21}$.
The second ratio is $21 : 93$, which can be written as the fraction $\frac{21}{93}$.
To compare the fractions $\frac{10}{21}$ and $\frac{21}{93}$, we can use the method of cross-multiplication. For two fractions $\frac{a}{b}$ and $\frac{c}{d}$, we compare $a \times d$ and $b \times c$.
- If $a \times d > b \times c$, then $\frac{a}{b} > \frac{c}{d}$.
- If $a \times d < b \times c$, then $\frac{a}{b} < \frac{c}{d}$.
- If $a \times d = b \times c$, then $\frac{a}{b} = \frac{c}{d}$.
For the fractions $\frac{10}{21}$ and $\frac{21}{93}$, we calculate the cross-products:
First cross-product: $10 \times 93$
$10 \times 93 = 930$
Second cross-product: $21 \times 21$
$21 \times 21 = 441$
Now, we compare the two cross-products:
$930$ and $441$.
Since $930 > 441$, it follows that $\frac{10}{21} > \frac{21}{93}$.
Therefore, the ratio $10 : 21$ is larger than the ratio $21 : 93$.
The final answer is 10 : 21.
Question 50. Reshma prepared 18kg of Burfi by mixing Khoya with sugar in the ratio of 7 : 2. How much Khoya did she use?
Answer:
Given:
Total amount of Burfi = 18 kg
Ratio of Khoya to sugar = 7 : 2
To Find:
Amount of Khoya used.
Solution:
The ratio of Khoya to sugar is 7:2. This means that for every 7 parts of Khoya, there are 2 parts of sugar in the Burfi mixture.
The total number of parts in the ratio is the sum of the parts of Khoya and sugar.
Total parts = Parts of Khoya + Parts of sugar
Total parts = $7 + 2 = 9$ parts.
The total amount of Burfi is 18 kg, which corresponds to the total number of parts (9 parts).
So, 9 parts = 18 kg.
To find the weight of one part, we divide the total weight by the total number of parts.
Weight of 1 part = $\frac{\text{Total weight of Burfi}}{\text{Total parts}}$
Weight of 1 part = $\frac{18 \text{ kg}}{9}$
Weight of 1 part = 2 kg.
The amount of Khoya used is represented by 7 parts in the ratio.
Amount of Khoya = Number of Khoya parts $\times$ Weight of 1 part
Amount of Khoya = $7 \times 2 \text{ kg}$
Amount of Khoya = 14 kg.
Thus, Reshma used 14 kg of Khoya to prepare 18 kg of Burfi.
The final answer is 14 kg.
Question 51. A line segment 56cm long is to be divided into two parts in the ratio of 2 : 5. Find the length of each part.
Answer:
Given:
Total length of the line segment = 56 cm
Ratio in which the segment is divided = 2 : 5
To Find:
The length of each part.
Solution:
The line segment is divided into two parts in the ratio 2:5. This means that the total length is divided into a total number of parts equal to the sum of the parts in the ratio.
Total parts in the ratio = $2 + 5 = 7$ parts.
The total length of the line segment (56 cm) corresponds to these 7 total parts.
Length of 7 parts = 56 cm.
To find the length of one part, we divide the total length by the total number of parts.
Length of 1 part = $\frac{\text{Total length}}{\text{Total parts}}$
Length of 1 part = $\frac{56 \text{ cm}}{7}$
Length of 1 part = 8 cm.
The first part corresponds to 2 parts in the ratio.
Length of the first part = Number of parts in the first part $\times$ Length of 1 part
Length of the first part = $2 \times 8 \text{ cm}$
Length of the first part = 16 cm.
The second part corresponds to 5 parts in the ratio.
Length of the second part = Number of parts in the second part $\times$ Length of 1 part
Length of the second part = $5 \times 8 \text{ cm}$
Length of the second part = 40 cm.
To verify, the sum of the lengths of the two parts should equal the total length:
$16 \text{ cm} + 40 \text{ cm} = 56 \text{ cm}$. This matches the given total length.
The lengths of the two parts are 16 cm and 40 cm.
The final answer is 16 cm and 40 cm.
Question 52. The number of milk teeth in human beings is 20 and the number of permanent teeth is 32. Find the ratio of the number of milk teeth to the number of permanent teeth.
Answer:
Given:
Number of milk teeth = 20
Number of permanent teeth = 32
To Find:
The ratio of the number of milk teeth to the number of permanent teeth.
Solution:
The ratio of the number of milk teeth to the number of permanent teeth is given by:
Ratio = Number of milk teeth : Number of permanent teeth
Ratio = 20 : 32
To express this ratio in its lowest form, we can write it as a fraction and simplify it by dividing the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 20 and 32 is 4.
Divide both terms of the ratio by 4:
$\frac{20}{32} = \frac{20 \div 4}{32 \div 4} = \frac{5}{8}$
So, the ratio of the number of milk teeth to the number of permanent teeth in lowest form is 5:8.
The final answer is 5:8.
Question 53. Sex ratio is defined as the number of females per 1000 males in the population. Find the sex ratio if there are 3732 females per 4000 males in a town.
Answer:
Given:
Number of females = 3732
Number of males = 4000
Definition of sex ratio: number of females per 1000 males.
To Find:
The sex ratio for the town.
Solution:
The sex ratio is the number of females per 1000 males. This means we need to find out how many females there would be if the male population was exactly 1000, assuming the ratio remains constant.
We can set up a proportion comparing the given ratio of females to males with the sex ratio (females per 1000 males).
Let the sex ratio be $x$. This represents the number of females per 1000 males.
The proportion is:
$\frac{\text{Number of females}}{\text{Number of males}} = \frac{\text{Sex ratio}}{\text{1000}}$
$\frac{3732}{4000} = \frac{x}{1000}$
To solve for $x$, we multiply both sides of the equation by 1000:
$x = \frac{3732}{4000} \times 1000$
$x = \frac{3732 \times 1000}{4000}$
Cancel out the common factors:
$x = \frac{3732 \times \cancel{1000}^{1}}{\cancel{4000}_{4}}$
$x = \frac{3732}{4}$
Now, we perform the division:
$3732 \div 4 = 933$
$x = 933$
This means there are 933 females per 1000 males.
The sex ratio is 933.
The final answer is 933.
Question 54. In a year, Ravi earns Rs 360000 and paid Rs 24000 as income tax. Find the ratio of his
(a) income to income tax.
(b) income tax to income after paying income tax.
Answer:
Given:
Ravi's annual income = $\textsf{₹}$ 360000
Ravi's annual income tax paid = $\textsf{₹}$ 24000
To Find:
The ratio of:
(a) income to income tax.
(b) income tax to income after paying income tax.
Solution:
First, let's calculate the income after paying income tax.
Income after tax = Total Income - Income Tax Paid
Income after tax = $\textsf{₹}$ 360000 - $\textsf{₹}$ 24000
Income after tax = $\textsf{₹}$ 336000
Now, let's calculate the ratios:
(a) Ratio of income to income tax:
Ratio = Income : Income Tax Paid
Ratio = $\textsf{₹}$ 360000 : $\textsf{₹}$ 24000
We can write this as a fraction:
Ratio = $\frac{360000}{24000}$
Cancel out the trailing zeros:
Ratio = $\frac{360}{24}$
Simplify the fraction by dividing the numerator and denominator by their GCD. Both are divisible by 12 (or by 2, then 12):
$\frac{360 \div 12}{24 \div 12} = \frac{30}{2}$
Now, divide by 2:
$\frac{30 \div 2}{2 \div 2} = \frac{15}{1}$
The ratio is 15:1.
(b) Ratio of income tax to income after paying income tax:
Ratio = Income Tax Paid : Income After Tax
Ratio = $\textsf{₹}$ 24000 : $\textsf{₹}$ 336000
We can write this as a fraction:
Ratio = $\frac{24000}{336000}$
Cancel out the trailing zeros:
Ratio = $\frac{24}{336}$
Simplify the fraction. Both are divisible by 24:
$\frac{24 \div 24}{336 \div 24} = \frac{1}{14}$
(We can perform the division $336 \div 24$ or factorize: $24 = 2 \times 12$, $336 = 28 \times 12$, so $\frac{24}{336} = \frac{2 \times 12}{28 \times 12} = \frac{2}{28} = \frac{1}{14}$)
The ratio is 1:14.
The ratio of his income to income tax is 15:1.
The ratio of his income tax to income after paying income tax is 1:14.
Question 55. Ramesh earns Rs 28000 per month. His wife Rama earns Rs 36000 per month. Find the ratio of
(a) Ramesh’s earnings to their total earnings
(b) Rama’s earnings to their total earnings.
Answer:
Given:
Ramesh’s monthly earnings = $\textsf{₹}$ 28000
Rama’s monthly earnings = $\textsf{₹}$ 36000
To Find:
The ratio of:
(a) Ramesh’s earnings to their total earnings
(b) Rama’s earnings to their total earnings.
Solution:
First, calculate their total monthly earnings.
Total earnings = Ramesh’s earnings + Rama’s earnings
Total earnings = $\textsf{₹}$ 28000 + $\textsf{₹}$ 36000
Total earnings = $\textsf{₹}$ 64000
Now, calculate the required ratios:
(a) Ratio of Ramesh’s earnings to their total earnings:
Ratio = Ramesh’s earnings : Total earnings
Ratio = $\textsf{₹}$ 28000 : $\textsf{₹}$ 64000
Write the ratio as a fraction:
Ratio = $\frac{28000}{64000}$
Cancel out the trailing zeros:
Ratio = $\frac{28}{64}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor (GCD). The GCD of 28 and 64 is 4.
$\frac{28 \div 4}{64 \div 4} = \frac{7}{16}$
The ratio is 7:16.
(b) Ratio of Rama’s earnings to their total earnings:
Ratio = Rama’s earnings : Total earnings
Ratio = $\textsf{₹}$ 36000 : $\textsf{₹}$ 64000
Write the ratio as a fraction:
Ratio = $\frac{36000}{64000}$
Cancel out the trailing zeros:
Ratio = $\frac{36}{64}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor (GCD). The GCD of 36 and 64 is 4.
$\frac{36 \div 4}{64 \div 4} = \frac{9}{16}$
The ratio is 9:16.
The ratio of Ramesh’s earnings to their total earnings is 7:16.
The ratio of Rama’s earnings to their total earnings is 9:16.
Question 56. Of the 288 persons working in a company, 112 are men and the remaining are women. Find the ratio of the number of
(a) men to that of women.
(b) men to the total number of persons.
(c) women to the total number of persons.
Answer:
Given:
Total number of persons in the company = 288
Number of men = 112
To Find:
The ratio of:
(a) men to women.
(b) men to total persons.
(c) women to total persons.
Solution:
First, find the number of women.
Number of women = Total number of persons - Number of men
Number of women = $288 - 112 = 176$
Now, calculate the required ratios:
(a) Ratio of the number of men to that of women:
Ratio = Number of men : Number of women
Ratio = 112 : 176
Write the ratio as a fraction and simplify by dividing by the GCD of 112 and 176, which is 16.
Ratio = $\frac{112}{176} = \frac{112 \div 16}{176 \div 16} = \frac{7}{11}$
The ratio is 7:11.
(b) Ratio of the number of men to the total number of persons:
Ratio = Number of men : Total number of persons
Ratio = 112 : 288
Write the ratio as a fraction and simplify by dividing by the GCD of 112 and 288, which is 16.
Ratio = $\frac{112}{288} = \frac{112 \div 16}{288 \div 16} = \frac{7}{18}$
The ratio is 7:18.
(c) Ratio of the number of women to the total number of persons:
Ratio = Number of women : Total number of persons
Ratio = 176 : 288
Write the ratio as a fraction and simplify by dividing by the GCD of 176 and 288, which is 16.
Ratio = $\frac{176}{288} = \frac{176 \div 16}{288 \div 16} = \frac{11}{18}$
The ratio is 11:18.
The ratio of the number of men to that of women is 7:11.
The ratio of the number of men to the total number of persons is 7:18.
The ratio of the number of women to the total number of persons is 11:18.
Question 57. A rectangular sheet of paper is of length 1.2m and width 21cm. Find the ratio of width of the paper to its length.
Answer:
Given:
Length of the rectangular sheet = 1.2 m
Width of the rectangular sheet = 21 cm
To Find:
The ratio of the width of the paper to its length.
Solution:
To find the ratio of two quantities, they must be in the same unit. The length is given in meters (m) and the width is given in centimeters (cm). We should convert one of the quantities so that both are in the same unit. Let's convert the length from meters to centimeters.
We know that $1 \text{ meter} = 100 \text{ centimeters}$.
Length $= 1.2 \text{ m} = 1.2 \times 100 \text{ cm} = 120 \text{ cm}$.
Now, both quantities are in centimeters:
Width = 21 cm
Length = 120 cm
The ratio of the width of the paper to its length is:
Ratio = Width : Length
Ratio = 21 cm : 120 cm
To express this ratio in its lowest form, we write it as a fraction and simplify it by dividing the numerator and denominator by their greatest common divisor (GCD).
Ratio = $\frac{21}{120}$
The GCD of 21 and 120 is 3. Divide both the numerator and the denominator by 3:
$\frac{21 \div 3}{120 \div 3} = \frac{7}{40}$
The ratio in the lowest form is 7:40.
The final answer is 7:40.
Question 58. A scooter travels 120km in 3 hours and a train travels 120km in 2 hours. Find the ratio of their speeds.
(Hint: $Speed = \frac{distance\; travelled}{time \;taken}$)
Answer:
Given:
Distance travelled by scooter = 120 km
Time taken by scooter = 3 hours
Distance travelled by train = 120 km
Time taken by train = 2 hours
To Find:
The ratio of the speeds of the scooter and the train.
Solution:
First, calculate the speed of the scooter using the given formula:
Speed of scooter $= \frac{\text{Distance travelled by scooter}}{\text{Time taken by scooter}}$
Speed of scooter $= \frac{120 \text{ km}}{3 \text{ hours}}$
Speed of scooter $= 40 \text{ km/hour}$.
Next, calculate the speed of the train:
Speed of train $= \frac{\text{Distance travelled by train}}{\text{Time taken by train}}$
Speed of train $= \frac{120 \text{ km}}{2 \text{ hours}}$
Speed of train $= 60 \text{ km/hour}$.
Now, find the ratio of the speed of the scooter to the speed of the train.
Ratio = Speed of scooter : Speed of train
Ratio = 40 km/hour : 60 km/hour
To express this ratio in its lowest form, we write it as a fraction and simplify it by dividing the numerator and denominator by their greatest common divisor (GCD).
Ratio = $\frac{40}{60}$
The GCD of 40 and 60 is 20. Divide both the numerator and the denominator by 20:
$\frac{40 \div 20}{60 \div 20} = \frac{2}{3}$
The ratio of their speeds in the lowest form is 2:3.
The final answer is 2:3.
Question 59. An office opens at 9 a.m. and closes at 5.30 p.m. with a lunch break of 30 minutes. What is the ratio of lunch break to the total period in the office?
Answer:
Given:
Office opening time = 9 a.m.
Office closing time = 5:30 p.m.
Lunch break duration = 30 minutes
To Find:
The ratio of lunch break to the total period in the office.
Solution:
First, calculate the total duration the office remains open from 9 a.m. to 5:30 p.m.
From 9 a.m. to 5 p.m. is 8 hours.
From 5 p.m. to 5:30 p.m. is 30 minutes.
Total duration = 8 hours + 30 minutes.
Convert the total duration to a single unit, minutes. We know that 1 hour = 60 minutes.
8 hours $= 8 \times 60 \text{ minutes} = 480 \text{ minutes}$.
Total duration $= 480 \text{ minutes} + 30 \text{ minutes} = 510 \text{ minutes}$.
The duration of the lunch break is given as 30 minutes.
The total period in the office is 510 minutes.
The ratio of the lunch break to the total period in the office is:
Ratio = Lunch break duration : Total duration
Ratio = 30 minutes : 510 minutes
To express this ratio in its lowest form, we write it as a fraction and simplify by dividing the numerator and denominator by their greatest common divisor (GCD).
Ratio = $\frac{30}{510}$
We can cancel out the trailing zero from both numbers:
Ratio = $\frac{3}{51}$
The GCD of 3 and 51 is 3. Divide both the numerator and the denominator by 3:
$\frac{3 \div 3}{51 \div 3} = \frac{1}{17}$
The ratio in the lowest form is 1:17.
The final answer is 1:17.
Question 60. The shadow of a 3m long stick is 4m long. At the same time of the day, if the shadow of a flagstaff is 24m long, how tall is the flagstaff?
Answer:
Given:
Length of stick = 3 m
Length of shadow of stick = 4 m
Length of shadow of flagstaff = 24 m
Time of day is the same for both measurements.
To Find:
The height of the flagstaff.
Solution:
At the same time of the day, the ratio of the height of an object to the length of its shadow is constant. This is because the angle of elevation of the sun is the same.
We can set up a proportion based on the ratio $\frac{\text{Height of object}}{\text{Length of shadow}}$.
For the stick:
Ratio $\frac{\text{Height}}{\text{Shadow}} = \frac{\text{Length of stick}}{\text{Length of shadow of stick}} = \frac{3 \text{ m}}{4 \text{ m}} = \frac{3}{4}$.
For the flagstaff, let the height be $h$ meters.
The shadow length is 24 m.
Ratio $\frac{\text{Height}}{\text{Shadow}} = \frac{\text{Height of flagstaff}}{\text{Length of shadow of flagstaff}} = \frac{h \text{ m}}{24 \text{ m}} = \frac{h}{24}$.
Since the time of day is the same, the ratios are equal:
$\frac{3}{4} = \frac{h}{24}$
... (i)
To solve for $h$, multiply both sides of the equation by 24:
$h = \frac{3}{4} \times 24$
$h = 3 \times \frac{24}{4}$
$h = 3 \times \cancel{6}$
$h = 18$
The height of the flagstaff is 18 meters.
The final answer is 18 m.
Question 61. A recipe calls for 1 cup of milk for every $2\frac{1}{2}$ cups of flour to make a cake that would feed 6persons. How many cups of both flour and milk will be needed to make a similar cake for 8 people?
Answer:
Given:
Ingredients for a cake for 6 people:
Milk = 1 cup
Flour = $2\frac{1}{2}$ cups
To Find:
The amount of milk and flour needed for a similar cake for 8 people.
Solution:
First, convert the mixed number for flour into an improper fraction:
$2\frac{1}{2} = 2 + \frac{1}{2} = \frac{4}{2} + \frac{1}{2} = \frac{4+1}{2} = \frac{5}{2}$ cups.
The ratio of milk to flour for a cake for 6 people is 1 cup : $\frac{5}{2}$ cups.
This ratio can be written as $\frac{1}{\frac{5}{2}} = 1 \times \frac{2}{5} = \frac{2}{5}$.
So, the ratio of milk to flour is 2:5.
Since we need to make a similar cake, the ratio of milk to flour will remain the same, 2:5.
The amount of ingredients is directly proportional to the number of people the cake serves.
Let the amount of milk needed for 8 people be $M$ cups.
Let the amount of flour needed for 8 people be $F$ cups.
Consider the ratio of milk needed to the number of people served:
For 6 people, milk needed = 1 cup.
Ratio $\frac{\text{Milk}}{\text{People}} = \frac{1 \text{ cup}}{6 \text{ people}} = \frac{1}{6}$.
For 8 people, milk needed = $M$ cups.
Ratio $\frac{\text{Milk}}{\text{People}} = \frac{M \text{ cups}}{8 \text{ people}} = \frac{M}{8}$.
Since the cake is similar, the ratio of milk per person is constant:
$\frac{1}{6} = \frac{M}{8}$
... (i)
Solve for $M$ by multiplying both sides by 8:
$M = \frac{1}{6} \times 8 = \frac{8}{6} = \frac{4}{3}$ cups.
Consider the ratio of flour needed to the number of people served:
For 6 people, flour needed = $\frac{5}{2}$ cups.
Ratio $\frac{\text{Flour}}{\text{People}} = \frac{\frac{5}{2} \text{ cups}}{6 \text{ people}} = \frac{5/2}{6} = \frac{5}{2 \times 6} = \frac{5}{12}$.
For 8 people, flour needed = $F$ cups.
Ratio $\frac{\text{Flour}}{\text{People}} = \frac{F \text{ cups}}{8 \text{ people}} = \frac{F}{8}$.
Since the cake is similar, the ratio of flour per person is constant:
$\frac{5}{12} = \frac{F}{8}$
... (ii)
Solve for $F$ by multiplying both sides by 8:
$F = \frac{5}{12} \times 8 = \frac{5 \times \cancel{8}^{2}}{\cancel{12}_{3}} = \frac{5 \times 2}{3} = \frac{10}{3}$ cups.
Alternatively, once we have the amount of milk ($M = \frac{4}{3}$ cups) for 8 people, we can use the milk to flour ratio (2:5) to find the amount of flour ($F$).
Ratio $\frac{\text{Milk}}{\text{Flour}} = \frac{M}{F} = \frac{2}{5}$.
Substitute $M = \frac{4}{3}$:
$\frac{4/3}{F} = \frac{2}{5}$
Cross-multiply:
$4/3 \times 5 = F \times 2$
$\frac{20}{3} = 2F$
Divide by 2:
$F = \frac{20/3}{2} = \frac{20}{3 \times 2} = \frac{20}{6} = \frac{10}{3}$ cups.
The amount of milk needed for 8 people is $\frac{4}{3}$ cups, and the amount of flour needed is $\frac{10}{3}$ cups.
These can also be written as mixed numbers: $\frac{4}{3} = 1\frac{1}{3}$ cups of milk, and $\frac{10}{3} = 3\frac{1}{3}$ cups of flour.
The final answer is $\frac{4}{3}$ cups of milk and $\frac{10}{3}$ cups of flour (or $1\frac{1}{3}$ cups of milk and $3\frac{1}{3}$ cups of flour).
Question 62. In a school, the ratio of the number of large classrooms to small classrooms is 3:4. If the number of small rooms is 20, then find the number of large rooms.
Answer:
Given:
Ratio of large classrooms to small classrooms = 3 : 4
Number of small classrooms = 20
To Find:
The number of large classrooms.
Solution:
Let the number of large classrooms be $L$ and the number of small classrooms be $S$.
The given ratio is $\frac{L}{S} = \frac{3}{4}$.
We are given that the number of small rooms $S = 20$.
Substitute the value of $S$ into the ratio equation:
$\frac{L}{20} = \frac{3}{4}$
... (i)
To solve for $L$, multiply both sides of the equation by 20:
$L = \frac{3}{4} \times 20$
$L = 3 \times \frac{20}{4}$
$L = 3 \times \cancel{5}$
$L = 15$
Thus, the number of large classrooms is 15.
The final answer is 15.
Question 63. Samira sells newspapers at Janpath crossing daily. On a particular day, she had 312 newspapers out of which 216 are in English and remaining in Hindi. Find the ratio of
(a) the number of English newspapers to the number of Hindi newspapers.
(b) the number of Hindi newspapers to the total number of newspapers.
Answer:
Given:
Total number of newspapers = 312
Number of English newspapers = 216
The remaining are in Hindi.
To Find:
The ratio of:
(a) English newspapers to Hindi newspapers.
(b) Hindi newspapers to the total number of newspapers.
Solution:
First, find the number of Hindi newspapers.
Number of Hindi newspapers = Total number of newspapers - Number of English newspapers
Number of Hindi newspapers = $312 - 216 = 96$
Now, calculate the required ratios:
(a) The ratio of the number of English newspapers to the number of Hindi newspapers:
Ratio = Number of English newspapers : Number of Hindi newspapers
Ratio = 216 : 96
Write the ratio as a fraction and simplify by dividing by their greatest common divisor (GCD).
Let's find the GCD of 216 and 96. We can divide by common factors repeatedly:
$\frac{216}{96} = \frac{216 \div 12}{96 \div 12} = \frac{18}{8}$ (Dividing by 12)
Now divide by 2:
$\frac{18 \div 2}{8 \div 2} = \frac{9}{4}$
The GCD of 216 and 96 is $12 \times 2 = 24$. We could have done $\frac{216 \div 24}{96 \div 24} = \frac{9}{4}$.
The ratio is 9:4.
(b) The ratio of the number of Hindi newspapers to the total number of newspapers:
Ratio = Number of Hindi newspapers : Total number of newspapers
Ratio = 96 : 312
Write the ratio as a fraction and simplify by dividing by their greatest common divisor (GCD).
We know that 96 is a factor of 312 divided by some number. Let's find the GCD of 96 and 312.
Divide by common factors repeatedly:
$\frac{96}{312} = \frac{96 \div 12}{312 \div 12} = \frac{8}{26}$ (Dividing by 12)
Now divide by 2:
$\frac{8 \div 2}{26 \div 2} = \frac{4}{13}$
The GCD of 96 and 312 is $12 \times 2 = 24$. We could have done $\frac{96 \div 24}{312 \div 24} = \frac{4}{13}$.
The ratio is 4:13.
The ratio of the number of English newspapers to the number of Hindi newspapers is 9:4.
The ratio of the number of Hindi newspapers to the total number of newspapers is 4:13.
Question 64. The students of a school belong to different religious backgrounds. The number of Hindu students is 288, the number of Muslim students is 252, the number of Sikh students is 144 and the number of Christian students is 72. Find the ratio of
(a) the number of Hindu students to the number of Christian students.
(b) the number of Muslim students to the total number of students.
Answer:
Given:
Number of Hindu students = 288
Number of Muslim students = 252
Number of Sikh students = 144
Number of Christian students = 72
To Find:
The ratio of:
(a) the number of Hindu students to the number of Christian students.
(b) the number of Muslim students to the total number of students.
Solution:
First, calculate the total number of students in the school.
Total number of students = Number of Hindu students + Number of Muslim students + Number of Sikh students + Number of Christian students
Total number of students = $288 + 252 + 144 + 72$
Total number of students = $540 + 144 + 72$
Total number of students = $684 + 72 = 756$
Total number of students = 756.
Now, calculate the required ratios:
(a) The ratio of the number of Hindu students to the number of Christian students:
Ratio = Number of Hindu students : Number of Christian students
Ratio = 288 : 72
Write the ratio as a fraction and simplify by dividing by their greatest common divisor (GCD). We can observe that 288 is a multiple of 72 ($72 \times 4 = 288$).
Ratio = $\frac{288}{72} = \frac{288 \div 72}{72 \div 72} = \frac{4}{1}$
The ratio is 4:1.
(b) The ratio of the number of Muslim students to the total number of students:
Ratio = Number of Muslim students : Total number of students
Ratio = 252 : 756
Write the ratio as a fraction and simplify by dividing by their greatest common divisor (GCD). We can try dividing by common factors.
Both are divisible by 4:
$\frac{252 \div 4}{756 \div 4} = \frac{63}{189}$
Both are divisible by 9:
$\frac{63 \div 9}{189 \div 9} = \frac{7}{21}$
Both are divisible by 7:
$\frac{7 \div 7}{21 \div 7} = \frac{1}{3}$
The GCD of 252 and 756 is $4 \times 9 \times 7 = 252$. We could have done $\frac{252 \div 252}{756 \div 252} = \frac{1}{3}$.
The ratio is 1:3.
The ratio of the number of Hindu students to the number of Christian students is 4:1.
The ratio of the number of Muslim students to the total number of students is 1:3.
Question 65. When Chinmay visted chowpati at Mumbai on a holiday, he observed that the ratio of North Indian food stalls to South Indian food stalls is 5:4. If the total number of food stalls is 117, find the number of each type of food stalls.
Answer:
Given:
Ratio of North Indian food stalls to South Indian food stalls = 5 : 4
Total number of food stalls = 117
To Find:
The number of North Indian food stalls and the number of South Indian food stalls.
Solution:
The ratio of North Indian food stalls to South Indian food stalls is 5:4. This means that for every 5 parts representing North Indian stalls, there are 4 parts representing South Indian stalls.
The total number of parts in the ratio is the sum of the parts for each type of stall.
Total parts = Parts of North Indian stalls + Parts of South Indian stalls
Total parts = $5 + 4 = 9$ parts.
The total number of food stalls is 117, which corresponds to the total number of parts (9 parts).
So, 9 parts = 117 stalls.
To find the number of stalls corresponding to one part, we divide the total number of stalls by the total number of parts.
Number of stalls per part = $\frac{\text{Total number of stalls}}{\text{Total parts}}$
Number of stalls per part = $\frac{117}{9}$
To perform the division:
$\begin{array}{r} 13 \\ 9{\overline{\smash{\big)}\,117}} \\ \underline{-~\phantom{()}(9)} \\ 27 \\ \underline{-~\phantom{()}(27)} \\ 0 \end{array}$
Number of stalls per part = 13.
The number of North Indian food stalls corresponds to 5 parts in the ratio.
Number of North Indian stalls = Number of North Indian parts $\times$ Number of stalls per part
Number of North Indian stalls = $5 \times 13 = 65$ stalls.
The number of South Indian food stalls corresponds to 4 parts in the ratio.
Number of South Indian stalls = Number of South Indian parts $\times$ Number of stalls per part
Number of South Indian stalls = $4 \times 13 = 52$ stalls.
To verify, the sum of the number of each type of stall should equal the total number of stalls:
$65 + 52 = 117$. This matches the given total number of stalls.
The number of North Indian food stalls is 65 and the number of South Indian food stalls is 52.
The final answer is 65 North Indian stalls and 52 South Indian stalls.
Question 66. At the parking stand of Ramleela ground, Kartik counted that there are 115 cycles, 75 scooters and 45 bikes. Find the ratio of the number of cycles to the total number of vehicles.
Questoin 67. A train takes 2 hours to travel from Ajmer to Jaipur, which are 130km apart. How much time will it take to travel from Delhi to Bhopal which are 780km apart if the train is travelling at the uniform speed?
Answer:
Solution for Question 66:
Given:
Number of cycles = 115
Number of scooters = 75
Number of bikes = 45
To Find:
The ratio of the number of cycles to the total number of vehicles.
Solution:
First, calculate the total number of vehicles at the parking stand.
Total number of vehicles = Number of cycles + Number of scooters + Number of bikes
Total number of vehicles = $115 + 75 + 45 = 190 + 45 = 235$
Total number of vehicles = 235.
Now, find the ratio of the number of cycles to the total number of vehicles.
Ratio = Number of cycles : Total number of vehicles
Ratio = 115 : 235
Write the ratio as a fraction and simplify by dividing by their greatest common divisor (GCD).
Ratio = $\frac{115}{235}$
Both numbers end in 5, so they are divisible by 5.
$\frac{115 \div 5}{235 \div 5} = \frac{23}{47}$
The numbers 23 and 47 are both prime numbers. Therefore, the ratio is in its lowest form.
The ratio is 23:47.
The final answer for Question 66 is 23:47.
Solution for Question 67:
Given:
Distance from Ajmer to Jaipur = 130 km
Time taken from Ajmer to Jaipur = 2 hours
Distance from Delhi to Bhopal = 780 km
The train is travelling at a uniform speed.
To Find:
Time taken to travel from Delhi to Bhopal.
Solution:
Since the train is travelling at a uniform speed, we can first calculate this speed using the information about the journey from Ajmer to Jaipur.
Speed $= \frac{\text{Distance travelled}}{\text{Time taken}}$
Speed $= \frac{130 \text{ km}}{2 \text{ hours}}$
Speed $= 65 \text{ km/hour}$.
Now, we can use this speed and the distance from Delhi to Bhopal to find the time taken for the second journey.
Time taken $= \frac{\text{Distance}}{\text{Speed}}$
Distance from Delhi to Bhopal = 780 km
Speed of the train = 65 km/hour
Time taken $= \frac{780 \text{ km}}{65 \text{ km/hour}}$
Time taken $= \frac{780}{65}$ hours.
Let's perform the division:
$\frac{780}{65} = \frac{\cancel{780}^{156}}{\cancel{65}_{13}}$ (Dividing by 5)
Now divide 156 by 13.
$\begin{array}{r} 12 \\ 13{\overline{\smash{\big)}\,156}} \\ \underline{-~\phantom{()}(13)} \\ 26 \\ \underline{-~\phantom{()}(26)} \\ 0 \end{array}$
So, $\frac{156}{13} = 12$.
Time taken = 12 hours.
It will take the train 12 hours to travel from Delhi to Bhopal.
The final answer for Question 67 is 12 hours.
Question 68. The length and breadth of a school ground are 150m and 90m respectively, while the length and breadth of a mela ground are 210m and 126m, respectively. Are these measurements in proportion?
Answer:
Given:
School ground: Length = 150 m, Breadth = 90 m
Mela ground: Length = 210 m, Breadth = 126 m
To Determine:
If these measurements are in proportion.
Solution:
The measurements are in proportion if the ratio of the length to the breadth for the school ground is equal to the ratio of the length to the breadth for the mela ground.
Calculate the ratio of length to breadth for the school ground:
Ratio (School) = Length of school ground : Breadth of school ground
Ratio (School) = 150 m : 90 m
Write the ratio as a fraction and simplify:
Ratio (School) = $\frac{150}{90} = \frac{\cancel{150}^{15}}{\cancel{90}_{9}} = \frac{15}{9}$ (Cancelling 10)
Divide by the GCD of 15 and 9, which is 3:
$\frac{15 \div 3}{9 \div 3} = \frac{5}{3}$
The ratio of length to breadth for the school ground is 5:3.
Calculate the ratio of length to breadth for the mela ground:
Ratio (Mela) = Length of mela ground : Breadth of mela ground
Ratio (Mela) = 210 m : 126 m
Write the ratio as a fraction and simplify:
Ratio (Mela) = $\frac{210}{126}$
Both are divisible by 6:
$\frac{210 \div 6}{126 \div 6} = \frac{35}{21}$
Both are divisible by 7:
$\frac{35 \div 7}{21 \div 7} = \frac{5}{3}$
The ratio of length to breadth for the mela ground is 5:3.
Now, compare the two ratios:
Ratio (School) = 5:3
Ratio (Mela) = 5:3
Since the ratio of the length to the breadth is the same for both grounds ($\frac{5}{3} = \frac{5}{3}$), the measurements are in proportion.
The final answer is Yes, the measurements are in proportion because the ratio of length to breadth for both grounds is the same (5:3).
Question 69. In Fig. 8.4, the comparative areas of the continents are given:
What is the ratio of the areas of
(a) Africa to Europe
(b) Australia to Asia
(c) Antarctica to Combined area of North America and South America.
Answer:
Solution:
Based on reading the comparative areas from the bar graph in Fig. 8.4, we have the following approximate values:
Area of Asia $\approx$ 4.5 units
Area of Africa $\approx$ 3.0 units
Area of North America $\approx$ 2.4 units
Area of South America $\approx$ 1.8 units
Area of Antarctica $\approx$ 1.4 units
Area of Europe $\approx$ 1.0 unit
Area of Australia $\approx$ 0.8 units
Now, we calculate the required ratios:
(a) Ratio of the areas of Africa to Europe:
Ratio = Area of Africa : Area of Europe
Ratio $\approx$ 3.0 : 1.0
Ratio $\approx \frac{3.0}{1.0} = \frac{3}{1}$
The ratio is 3:1.
(b) Ratio of the areas of Australia to Asia:
Ratio = Area of Australia : Area of Asia
Ratio $\approx$ 0.8 : 4.5
Ratio $\approx \frac{0.8}{4.5}$
To remove decimals, multiply the numerator and denominator by 10:
Ratio $\approx \frac{0.8 \times 10}{4.5 \times 10} = \frac{8}{45}$
The numbers 8 and 45 have no common factors other than 1. The ratio is in its lowest form.
The ratio is 8:45.
(c) Ratio of Antarctica to Combined area of North America and South America:
Combined area of North America and South America = Area of North America + Area of South America
Combined area $\approx$ 2.4 units + 1.8 units = 4.2 units.
Ratio = Area of Antarctica : Combined area of North America and South America
Ratio $\approx$ 1.4 : 4.2
Ratio $\approx \frac{1.4}{4.2}$
To remove decimals, multiply the numerator and denominator by 10:
Ratio $\approx \frac{1.4 \times 10}{4.2 \times 10} = \frac{14}{42}$
Simplify the fraction by dividing the numerator and denominator by their GCD, which is 14:
$\frac{14 \div 14}{42 \div 14} = \frac{1}{3}$
The ratio is 1:3.
The ratio of the areas of Africa to Europe is 3:1.
The ratio of the areas of Australia to Asia is 8:45.
The ratio of Antarctica to Combined area of North America and South America is 1:3.
Question 70. A tea merchant blends two varieties of tea costing her Rs 234 and Rs 130 per kg in the ratio of their costs. If the weight of the mixture is 84kg, then find the weight of each variety of tea.
Answer:
Given:
Cost of Variety 1 tea = $\textsf{₹}$ 234 per kg
Cost of Variety 2 tea = $\textsf{₹}$ 130 per kg
The two varieties are blended in the ratio of their costs.
Total weight of the mixture = 84 kg
To Find:
The weight of each variety of tea in the mixture.
Solution:
The ratio of the costs of the two varieties of tea is:
Ratio of costs = Cost of Variety 1 : Cost of Variety 2
Ratio of costs = $\textsf{₹}$ 234 : $\textsf{₹}$ 130
The two varieties of tea are blended in the ratio of their costs, which means the ratio of their weights in the mixture is equal to the ratio of their costs.
Ratio of weights (Variety 1 : Variety 2) = Ratio of costs (Variety 1 : Variety 2)
Ratio of weights = 234 : 130
Simplify the ratio 234:130 by dividing both numbers by their greatest common divisor (GCD).
Both numbers are divisible by 2:
$\frac{234 \div 2}{130 \div 2} = \frac{117}{65}$
Now check for common factors of 117 and 65. 117 = $9 \times 13$, 65 = $5 \times 13$. The GCD is 13.
$\frac{117 \div 13}{65 \div 13} = \frac{9}{5}$
The simplified ratio of the weights is 9:5. This means for every 9 parts of Variety 1 tea, there are 5 parts of Variety 2 tea in the mixture.
The total number of parts in the ratio of weights is:
Total parts = 9 parts (Variety 1) + 5 parts (Variety 2) = 14 parts.
The total weight of the mixture is 84 kg, which corresponds to the total number of parts (14 parts).
So, 14 parts = 84 kg.
To find the weight corresponding to one part, divide the total weight by the total number of parts.
Weight of 1 part = $\frac{\text{Total weight of mixture}}{\text{Total parts}}$
Weight of 1 part = $\frac{84 \text{ kg}}{14}$
$84 \div 14 = 6$
Weight of 1 part = 6 kg.
The weight of Variety 1 tea corresponds to 9 parts in the ratio.
Weight of Variety 1 = Number of Variety 1 parts $\times$ Weight of 1 part
Weight of Variety 1 = $9 \times 6 \text{ kg} = 54 \text{ kg}$.
The weight of Variety 2 tea corresponds to 5 parts in the ratio.
Weight of Variety 2 = Number of Variety 2 parts $\times$ Weight of 1 part
Weight of Variety 2 = $5 \times 6 \text{ kg} = 30 \text{ kg}$.
To verify, the sum of the weights of the two varieties should equal the total weight:
$54 \text{ kg} + 30 \text{ kg} = 84 \text{ kg}$. This matches the given total weight.
The weight of the first variety of tea is 54 kg and the weight of the second variety of tea is 30 kg.
The final answer is 54 kg of Variety 1 tea and 30 kg of Variety 2 tea.
Question 71. An alloy contains only zinc and copper and they are in the ratio of 7:9. If the weight of the alloy is 8kg, then find the weight of copper in the alloy
Answer:
Given:
Ratio of zinc to copper in the alloy = 7 : 9
Total weight of the alloy = 8 kg
To Find:
The weight of copper in the alloy.
Solution:
The ratio of zinc to copper is 7:9. This means that for every 7 parts of zinc, there are 9 parts of copper in the alloy.
The total number of parts in the ratio is the sum of the parts of zinc and copper.
Total parts = Parts of zinc + Parts of copper
Total parts = $7 + 9 = 16$ parts.
The total weight of the alloy is 8 kg, which corresponds to the total number of parts (16 parts).
So, 16 parts = 8 kg.
To find the weight corresponding to one part, we divide the total weight by the total number of parts.
Weight of 1 part = $\frac{\text{Total weight of alloy}}{\text{Total parts}}$
Weight of 1 part = $\frac{8 \text{ kg}}{16}$
Weight of 1 part = $\frac{1}{2} \text{ kg}$ or 0.5 kg.
The weight of copper in the alloy corresponds to 9 parts in the ratio.
Weight of copper = Number of copper parts $\times$ Weight of 1 part
Weight of copper = $9 \times \frac{1}{2} \text{ kg} = \frac{9}{2} \text{ kg}$
Weight of copper = 4.5 kg.
Thus, the weight of copper in the 8 kg alloy is 4.5 kg.
The final answer is 4.5 kg (or $\frac{9}{2}$ kg).
Question 72. In the following figure, each division represents 1cm:

Express numerically the ratios of the following distances:
(i) AC : AF
(ii) AG : AD
(iii) BF : AI
(iv) CE : DI
Answer:
Given:
A number line with points A, B, C, D, E, F, G, H, I, J.
Each division represents 1 cm.
To Find:
The numerical ratios of the given distances.
Solution:
We first determine the length of each segment by counting the number of divisions between the two points. Since each division is 1 cm, the length of a segment is equal to the number of divisions between its endpoints in cm.
Assuming A is the starting point (0 or reference point), let's find the position of each point:
A = 0 cm
B = 1 cm
C = 2 cm
D = 3 cm
E = 4 cm
F = 5 cm
G = 6 cm
H = 7 cm
I = 8 cm
J = 9 cm
The length of a segment between two points, say X and Y, is given by the absolute difference of their positions: Length XY = $|Position(Y) - Position(X)|$.
(i) AC : AF
Length AC = Position(C) - Position(A) = 2 cm - 0 cm = 2 cm.
Length AF = Position(F) - Position(A) = 5 cm - 0 cm = 5 cm.
Ratio AC : AF = 2 cm : 5 cm = 2 : 5.
(ii) AG : AD
Length AG = Position(G) - Position(A) = 6 cm - 0 cm = 6 cm.
Length AD = Position(D) - Position(A) = 3 cm - 0 cm = 3 cm.
Ratio AG : AD = 6 cm : 3 cm = 6 : 3.
Simplify the ratio:
$\frac{6}{3} = \frac{2}{1}$
The ratio is 2:1.
(iii) BF : AI
Length BF = Position(F) - Position(B) = 5 cm - 1 cm = 4 cm.
Length AI = Position(I) - Position(A) = 8 cm - 0 cm = 8 cm.
Ratio BF : AI = 4 cm : 8 cm = 4 : 8.
Simplify the ratio:
$\frac{4}{8} = \frac{1}{2}$
The ratio is 1:2.
(iv) CE : DI
Length CE = Position(E) - Position(C) = 4 cm - 2 cm = 2 cm.
Length DI = Position(I) - Position(D) = 8 cm - 3 cm = 5 cm.
Ratio CE : DI = 2 cm : 5 cm = 2 : 5.
The ratio AC : AF is 2:5.
The ratio AG : AD is 2:1.
The ratio BF : AI is 1:2.
The ratio CE : DI is 2:5.
Question 73. Find two numbers whose sum is 100 and whose ratio is 9 :16.
Answer:
Given:
The sum of two numbers is 100.
The ratio of the two numbers is 9 : 16.
To Find:
The two numbers.
Solution:
Let the two numbers be $a$ and $b$.
According to the problem, their sum is 100:
$a + b = 100$
... (i)
The ratio of the two numbers is 9 : 16. This means $\frac{a}{b} = \frac{9}{16}$.
We can represent the numbers based on the ratio. Let the common ratio be $k$. Then the first number can be $9k$ and the second number can be $16k$.
First number = $9k$
Second number = $16k$
Substitute these expressions into the sum equation (i):
$9k + 16k = 100$
Combine the terms with $k$:
$(9 + 16)k = 100$
$25k = 100$
Solve for $k$ by dividing both sides by 25:
$k = \frac{100}{25}$
$k = 4$
Now substitute the value of $k$ back into the expressions for the two numbers:
First number = $9k = 9 \times 4 = 36$.
Second number = $16k = 16 \times 4 = 64$.
Let's verify the conditions:
Sum of the numbers = $36 + 64 = 100$. (Correct)
Ratio of the numbers = $36 : 64 = \frac{36}{64} = \frac{\cancel{36}^{9}}{\cancel{64}_{16}} = \frac{9}{16}$. (Correct)
The two numbers are 36 and 64.
The final answer is 36 and 64.
Question 74. In Fig. 8.6 (i) and Fig. 8.6 (ii), find the ratio of the area of the shaded portion to that of the whole figure:

Answer:
To find the ratio of the area of the shaded portion to the area of the whole figure, we need to count the number of shaded parts and the total number of equal parts in each figure.
For Fig. 8.6 (i):
This figure is a rectangle divided into equal smaller rectangles.
Count the number of rows and columns to find the total number of equal parts.
Number of rows = 5
Number of columns = 3
Total number of equal parts = $5 \times 3 = 15$.
Count the number of shaded parts.
Number of shaded parts = 6.
The ratio of the area of the shaded portion to that of the whole figure is:
Ratio = $\frac{\text{Number of shaded parts}}{\text{Total number of parts}}$
Ratio = $\frac{6}{15}$
Simplify the ratio by dividing the numerator and denominator by their greatest common divisor (GCD), which is 3.
$\frac{6 \div 3}{15 \div 3} = \frac{2}{5}$
The ratio is 2:5.
For Fig. 8.6 (ii):
This figure is a rectangle divided into equal smaller triangular parts. The rectangle consists of a grid of squares, and each square is divided into two equal triangles by a diagonal.
Count the number of rows and columns of the squares.
Number of rows of squares = 4
Number of columns of squares = 4
Total number of squares = $4 \times 4 = 16$.
Each square is divided into 2 equal triangles. So, the total number of equal triangular parts is $16 \times 2 = 32$.
Count the number of shaded triangular parts.
In each row, there are 4 shaded triangles.
Number of shaded rows = 4.
Total number of shaded parts = Number of shaded rows $\times$ Triangles per shaded row = $4 \times 4 = 16$.
The ratio of the area of the shaded portion to that of the whole figure is:
Ratio = $\frac{\text{Number of shaded parts}}{\text{Total number of parts}}$
Ratio = $\frac{16}{32}$
Simplify the ratio by dividing the numerator and denominator by their greatest common divisor (GCD), which is 16.
$\frac{16 \div 16}{32 \div 16} = \frac{1}{2}$
The ratio is 1:2.
The ratio of the area of the shaded portion to that of the whole figure for Fig. 8.6 (i) is 2:5.
The ratio of the area of the shaded portion to that of the whole figure for Fig. 8.6 (ii) is 1:2.
Question 75. A typist has to type a manuscript of 40 pages. She has typed 30 pages of the manuscript. What is the ratio of the number of pages typed to the number of pages left?
Answer:
Total number of pages in the manuscript = 40
Number of pages typed = 30
To Find:
The ratio of the number of pages typed to the number of pages left.
Solution:
First, find the number of pages left to be typed.
Number of pages left = Total number of pages - Number of pages typed
Number of pages left = $40 - 30 = 10$ pages.
Now, find the ratio of the number of pages typed to the number of pages left.
Ratio = Number of pages typed : Number of pages left
Ratio = 30 pages : 10 pages
To express this ratio in its lowest form, we write it as a fraction and simplify by dividing the numerator and denominator by their greatest common divisor (GCD), which is 10.
Ratio = $\frac{30}{10} = \frac{\cancel{30}^{3}}{\cancel{10}_{1}} = \frac{3}{1}$
The ratio is 3:1.
The final answer is 3:1.
Question 76. In a floral design made from tiles each of dimensions 40cm by 60cm (See Fig. 8.7), find the ratios of:
(a) the perimeter of shaded portion to the perimeter of the whole design.
(b) the area of the shaded portion to the area of the unshaded portion.
Answer:
Given:
Dimensions of each tile: Length = 60 cm, Breadth = 40 cm.
The design is made of several such tiles arranged in a rectangle.
Observation from Fig. 8.7:
The whole design is a rectangle made of $3 \times 2 = 6$ tiles.
The length of the whole design is $3 \times 60 \text{ cm} = 180 \text{ cm}$.
The breadth of the whole design is $2 \times 40 \text{ cm} = 80 \text{ cm}$.
There are 3 shaded tiles and 3 unshaded tiles.
To Find:
(a) The ratio of the perimeter of the shaded portion to the perimeter of the whole design.
(b) The ratio of the area of the shaded portion to the area of the unshaded portion.
Solution for (a) Perimeter:
The perimeter of the whole design is the perimeter of the outer rectangle with length 180 cm and breadth 80 cm.
Perimeter of whole design $= 2 \times (\text{Length} + \text{Breadth})$
Perimeter of whole design $= 2 \times (180 \text{ cm} + 80 \text{ cm})$
Perimeter of whole design $= 2 \times 260 \text{ cm} = 520 \text{ cm}$.
The shaded portion is formed by three adjacent tiles. Looking at the figure, the shaded tiles form an L-shape.
The perimeter of the shaded portion is the length of its boundary.
Tracing the boundary of the shaded portion:
- Horizontal segments: $60 \text{ cm} + 60 \text{ cm} + 40 \text{ cm} = 160 \text{ cm}$. (Outer top, outer bottom left, inner horizontal)
- Vertical segments: $40 \text{ cm} + 40 \text{ cm} + 60 \text{ cm} = 140 \text{ cm}$. (Outer left, outer bottom right, inner vertical)
Let's trace carefully:
Starting from the top-left corner of the shaded area and moving clockwise:
$60 \text{ cm}$ (top edge of left shaded tile)
$40 \text{ cm}$ (right edge of top-left shaded tile)
$60 \text{ cm}$ (top edge of top-right shaded tile)
$40 \text{ cm}$ (right edge of top-right shaded tile)
$60 \text{ cm}$ (bottom edge of bottom-right shaded tile)
$40 \text{ cm}$ (left edge of bottom-right shaded tile)
$60 \text{ cm}$ (bottom edge of bottom-left shaded tile)
$40 \text{ cm}$ (left edge of bottom-left shaded tile)
Perimeter of shaded portion $= 60 + 40 + 60 + 40 + 60 + 40 + 60 + 40 = 4 \times (60+40) = 4 \times 100 = 400$ cm? No, this assumes the shape is a rectangle, which it is not.
Let's trace again, identifying segments based on tile edges:
Outer boundary segments of shaded area:
- Top edge: $60 \text{ cm} + 60 \text{ cm} = 120 \text{ cm}$ (top edge of the top row of shaded tiles)
- Right edge: $40 \text{ cm} + 40 \text{ cm} = 80 \text{ cm}$ (right edge of the right column of shaded tiles)
- Bottom edge: $60 \text{ cm}$ (bottom edge of the bottom shaded tile)
- Left edge: $40 \text{ cm} + 40 \text{ cm} = 80 \text{ cm}$ (left edge of the left column of shaded tiles)
Inner boundary segments between shaded and unshaded area:
- Horizontal: $60 \text{ cm}$ (between top-right shaded and bottom-right unshaded)
- Vertical: $40 \text{ cm}$ (between bottom-left shaded and bottom-middle unshaded)
Perimeter of shaded portion = Sum of all boundary segments.
Perimeter of shaded portion $= 120 \text{ cm} + 80 \text{ cm} + 60 \text{ cm} + 80 \text{ cm} + 60 \text{ cm} + 40 \text{ cm} = 440 \text{ cm}$.
Ratio (Perimeter) = Perimeter of shaded portion : Perimeter of whole design
Ratio (Perimeter) = 440 cm : 520 cm
Ratio (Perimeter) = $\frac{440}{520} = \frac{44}{52}$ (Cancelling 10)
Divide by the GCD of 44 and 52, which is 4.
$\frac{44 \div 4}{52 \div 4} = \frac{11}{13}$
The ratio is 11:13.
Solution for (b) Area:
Area of each tile = Length $\times$ Breadth = $60 \text{ cm} \times 40 \text{ cm} = 2400 \text{ cm}^2$.
Area of the shaded portion = Number of shaded tiles $\times$ Area of one tile
Area of shaded portion = $3 \times 2400 \text{ cm}^2 = 7200 \text{ cm}^2$.
Area of the unshaded portion = Number of unshaded tiles $\times$ Area of one tile
Area of unshaded portion = $3 \times 2400 \text{ cm}^2 = 7200 \text{ cm}^2$.
The ratio of the area of the shaded portion to the area of the unshaded portion is:
Ratio (Area) = Area of shaded portion : Area of unshaded portion
Ratio (Area) = 7200 $\text{ cm}^2$ : 7200 $\text{ cm}^2$
Ratio (Area) = $\frac{7200}{7200} = \frac{1}{1}$
The ratio is 1:1.
The ratio of the perimeter of shaded portion to the perimeter of the whole design is 11:13.
The ratio of the area of the shaded portion to the area of the unshaded portion is 1:1.
Question 77. In Fig. 8.8, what is the ratio of the areas of
(a) shaded portion I to shaded portion II ?
(b) shaded portion II to shaded portion III?
(c) shaded portions I and II taken together and shaded portion III?
Answer:
To find the ratio of areas in Fig. 8.8, we can count the number of small squares that make up each shaded portion, assuming each small square has an area of 1 unit.
Count the number of squares in each shaded portion:
Shaded portion I (top-left): Count the squares. It forms a rectangle with 3 rows and 2 columns.
Area of shaded portion I = $3 \times 2 = 6$ square units.
Shaded portion II (top-right): Count the squares. It forms a rectangle with 3 rows and 3 columns.
Area of shaded portion II = $3 \times 3 = 9$ square units.
Shaded portion III (bottom): Count the squares. It forms a rectangle with 3 rows and 5 columns.
Area of shaded portion III = $3 \times 5 = 15$ square units.
Now, calculate the required ratios:
(a) Ratio of the areas of shaded portion I to shaded portion II:
Ratio = Area of Shaded Portion I : Area of Shaded Portion II
Ratio = 6 square units : 9 square units
Ratio = 6 : 9
Simplify the ratio by dividing by their GCD, which is 3.
Ratio = $\frac{6 \div 3}{9 \div 3} = \frac{2}{3}$
The ratio is 2:3.
(b) Ratio of the areas of shaded portion II to shaded portion III:
Ratio = Area of Shaded Portion II : Area of Shaded Portion III
Ratio = 9 square units : 15 square units
Ratio = 9 : 15
Simplify the ratio by dividing by their GCD, which is 3.
Ratio = $\frac{9 \div 3}{15 \div 3} = \frac{3}{5}$
The ratio is 3:5.
(c) Ratio of shaded portions I and II taken together and shaded portion III:
Area of shaded portions I and II taken together = Area of Shaded Portion I + Area of Shaded Portion II
Area of shaded portions I and II = $6 + 9 = 15$ square units.
Ratio = Area of (Shaded Portion I + Shaded Portion II) : Area of Shaded Portion III
Ratio = 15 square units : 15 square units
Ratio = 15 : 15
Simplify the ratio by dividing by their GCD, which is 15.
Ratio = $\frac{15 \div 15}{15 \div 15} = \frac{1}{1}$
The ratio is 1:1.
The ratio of the areas of shaded portion I to shaded portion II is 2:3.
The ratio of the areas of shaded portion II to shaded portion III is 3:5.
The ratio of shaded portions I and II taken together and shaded portion III is 1:1.
Question 78. A car can travel 240km in 15 litres of petrol. How much distance will it travel in 25 litres of petrol?
Answer:
Given:
Distance travelled in 15 litres of petrol = 240 km
To Find:
The distance the car will travel in 25 litres of petrol.
Solution:
Assuming the car travels at a constant rate of petrol consumption, the distance travelled is directly proportional to the amount of petrol consumed.
We can find the distance travelled per litre of petrol (mileage).
Distance per litre = $\frac{\text{Distance travelled}}{\text{Amount of petrol}}$
Distance per litre = $\frac{240 \text{ km}}{15 \text{ litres}}$
Calculate the division:
$\frac{240}{15}$
Divide 240 by 15. We know $15 \times 10 = 150$, and $240 - 150 = 90$. $15 \times 6 = 90$. So $15 \times (10+6) = 15 \times 16 = 240$.
Distance per litre = 16 km/litre.
Now, use this mileage to find the distance travelled in 25 litres of petrol.
Distance travelled = Mileage $\times$ Amount of petrol
Distance travelled = $16 \text{ km/litre} \times 25 \text{ litres}$
Distance travelled = $16 \times 25$ km.
Calculate $16 \times 25$:
$16 \times 25 = (4 \times 4) \times 25 = 4 \times (4 \times 25) = 4 \times 100 = 400$.
Alternatively, using multiplication array:
$\begin{array}{cc}& & 1 & 6 \\ \times & & 2 & 5 \\ \hline && 8 & 0 \\ & 3 & 2 & \times \\ \hline & 4 & 0 & 0 \\ \hline \end{array}$
Distance travelled = 400 km.
Alternatively, using proportion:
Let the distance travelled in 25 litres be $d$ km.
The ratio of distance to petrol is constant:
$\frac{\text{Distance}_1}{\text{Petrol}_1} = \frac{\text{Distance}_2}{\text{Petrol}_2}$
$\frac{240 \text{ km}}{15 \text{ litres}} = \frac{d \text{ km}}{25 \text{ litres}}$
... (i)
$\frac{240}{15} = \frac{d}{25}$
Multiply both sides by 25:
$d = \frac{240}{15} \times 25$
$d = 16 \times 25$
$d = 400$ km.
The car will travel 400 km in 25 litres of petrol.
The final answer is 400 km.
Question 79. Bachhu Manjhi earns Rs 24000 in 8 months. At this rate,
(a) how much does he earn in one year?
(b) in how many months does he earn Rs 42000?
Answer:
Given:
Earnings in 8 months = $\textsf{₹}$ 24000
Assume the earning rate is constant.
To Find:
(a) Earnings in one year.
(b) Number of months to earn $\textsf{₹}$ 42000.
Solution:
First, find the earning per month (monthly rate).
Earning per month = $\frac{\text{Total earnings}}{\text{Number of months}}$
Earning per month = $\frac{\textsf{₹ } 24000}{8 \text{ months}}$
Calculate the division:
$\frac{24000}{8} = \frac{24 \times 1000}{8} = \cancel{3} \times 1000 = 3000$.
Earning per month = $\textsf{₹}$ 3000.
(a) How much does he earn in one year?
One year has 12 months.
Earnings in one year = Earning per month $\times$ Number of months in a year
Earnings in one year = $\textsf{₹ } 3000 \text{/month} \times 12 \text{ months}$
Earnings in one year = $\textsf{₹ } (3000 \times 12)$
$3000 \times 12 = 3 \times 1000 \times 12 = 3 \times 12 \times 1000 = 36 \times 1000 = 36000$.
Earnings in one year = $\textsf{₹}$ 36000.
(b) In how many months does he earn Rs 42000?
Let $m$ be the number of months required to earn $\textsf{₹}$ 42000.
Using the monthly earning rate:
Total earnings = Earning per month $\times$ Number of months
$\textsf{₹ } 42000 = \textsf{₹ } 3000 \text{/month} \times m \text{ months}$
Solve for $m$:
$m = \frac{42000}{3000}$
Cancel out the trailing zeros:
$m = \frac{42}{3}$
$42 \div 3 = 14$.
$m = 14$ months.
Alternatively, using proportion:
The ratio of earnings to months is constant.
$\frac{\text{Earnings}_1}{\text{Months}_1} = \frac{\text{Earnings}_2}{\text{Months}_2}$
$\frac{\textsf{₹ } 24000}{8 \text{ months}} = \frac{\textsf{₹ } 42000}{m \text{ months}}$
$\frac{24000}{8} = \frac{42000}{m}$
$\frac{3000}{1} = \frac{42000}{m}$
$3000m = 42000$
$m = \frac{42000}{3000} = \frac{42}{3} = 14$ months.
In one year, he earns $\textsf{₹}$ 36000.
He earns $\textsf{₹}$ 42000 in 14 months.
Question 80. The yield of wheat from 8 hectares of land is 360 quintals. Find the number of hectares of land required for a yield of 540 quintals?
Answer:
Given:
Yield of wheat from 8 hectares = 360 quintals
Assume the yield rate per hectare is constant.
To Find:
The number of hectares of land required for a yield of 540 quintals.
Solution:
The yield of wheat is directly proportional to the area of land. This means the ratio of yield to land area is constant.
We can find the yield per hectare.
Yield per hectare = $\frac{\text{Total yield}}{\text{Area of land}}$
Yield per hectare = $\frac{360 \text{ quintals}}{8 \text{ hectares}}$
Calculate the division:
$\frac{360}{8}$
$360 \div 8 = (320 + 40) \div 8 = 320 \div 8 + 40 \div 8 = 40 + 5 = 45$.
Yield per hectare = 45 quintals/hectare.
Now, use this yield per hectare to find the area of land required for a yield of 540 quintals.
Area of land = $\frac{\text{Required yield}}{\text{Yield per hectare}}$
Area of land = $\frac{540 \text{ quintals}}{45 \text{ quintals/hectare}}$
Area of land = $\frac{540}{45}$ hectares.
Calculate the division:
$\frac{540}{45}$
Both numbers are divisible by 5:
$\frac{540 \div 5}{45 \div 5} = \frac{108}{9}$
Now, divide 108 by 9:
$108 \div 9 = 12$.
Area of land = 12 hectares.
Alternatively, using proportion:
Let $h$ be the number of hectares required for a yield of 540 quintals.
The ratio of yield to area is constant:
$\frac{\text{Yield}_1}{\text{Area}_1} = \frac{\text{Yield}_2}{\text{Area}_2}$
$\frac{360 \text{ quintals}}{8 \text{ hectares}} = \frac{540 \text{ quintals}}{h \text{ hectares}}$
... (i)
$\frac{360}{8} = \frac{540}{h}$
Simplify the left side: $\frac{360}{8} = 45$.
$45 = \frac{540}{h}$
Multiply both sides by $h$ and divide by 45:
$45h = 540$
$h = \frac{540}{45}$
$h = 12$ hectares.
12 hectares of land are required for a yield of 540 quintals.
The final answer is 12 hectares.
Question 81. The earth rotates 360o about its axis in about 24 hours. By how much degree will it rotate in 2 hours?
Answer:
Given:
Rotation in 24 hours = $360^\circ$
Assume the rate of rotation is constant.
To Find:
The degree of rotation in 2 hours.
Solution:
The degree of rotation is directly proportional to the time taken. This means the ratio of rotation angle to time is constant.
We can find the rate of rotation in degrees per hour.
Rotation rate = $\frac{\text{Total rotation angle}}{\text{Time taken}}$
Rotation rate = $\frac{360^\circ}{24 \text{ hours}}$
Calculate the division:
$\frac{360}{24}$
We know $24 \times 10 = 240$. $360 - 240 = 120$. $24 \times 5 = 120$. So, $24 \times (10+5) = 24 \times 15 = 360$.
Rotation rate = $15^\circ$ per hour.
Now, use this rotation rate to find the degree of rotation in 2 hours.
Rotation in 2 hours = Rotation rate $\times$ Time taken
Rotation in 2 hours = $15^\circ \text{/hour} \times 2 \text{ hours}$
Rotation in 2 hours = $15 \times 2$ degrees
Rotation in 2 hours = $30^\circ$.
Alternatively, using proportion:
Let $\theta$ be the degree of rotation in 2 hours.
The ratio of rotation angle to time is constant:
$\frac{\text{Rotation}_1}{\text{Time}_1} = \frac{\text{Rotation}_2}{\text{Time}_2}$
$\frac{360^\circ}{24 \text{ hours}} = \frac{\theta^\circ}{2 \text{ hours}}$
... (i)
$\frac{360}{24} = \frac{\theta}{2}$
Simplify the left side: $\frac{360}{24} = 15$.
$15 = \frac{\theta}{2}$
Multiply both sides by 2:
$\theta = 15 \times 2$
$\theta = 30$ degrees.
The earth will rotate by $30^\circ$ in 2 hours.
The final answer is $30^\circ$.
Question 82. Shivangi is suffering from anaemia as haemoglobin level in her blood is lower than the normal range. Doctor advised her to take one iron tablet two times a day. If the cost of 10 tablets is Rs 17, then what amount will she be required to pay for her medical bill for 15 days?
Answer:
Given:
Number of iron tablets per day = 1 tablet, 2 times a day = $1 \times 2 = 2$ tablets.
Cost of 10 tablets = $\textsf{₹}$ 17
Duration of treatment = 15 days
To Find:
Total amount to pay for the medical bill for 15 days.
Solution:
First, calculate the total number of tablets Shivangi needs for 15 days.
Number of tablets per day = 2 tablets.
Total number of tablets needed = Number of tablets per day $\times$ Number of days
Total number of tablets needed = $2 \times 15 = 30$ tablets.
Next, find the cost per tablet using the given information about the cost of 10 tablets.
Cost of 10 tablets = $\textsf{₹}$ 17.
Cost per tablet = $\frac{\text{Cost of 10 tablets}}{\text{Number of tablets}}$
Cost per tablet = $\frac{\textsf{₹ } 17}{10 \text{ tablets}}$
Cost per tablet = $\textsf{₹ } 1.70$ per tablet.
Now, calculate the total cost for 30 tablets.
Total cost = Number of tablets needed $\times$ Cost per tablet
Total cost = $30 \times \textsf{₹ } 1.70$
$30 \times 1.7 = 30 \times \frac{17}{10} = \frac{30 \times 17}{10} = \cancel{3} \times 17 = 51$.
Total cost = $\textsf{₹}$ 51.
Alternatively, using proportion:
The ratio of cost to the number of tablets is constant.
Let $C$ be the total cost for 30 tablets.
$\frac{\text{Cost}_1}{\text{Tablets}_1} = \frac{\text{Cost}_2}{\text{Tablets}_2}$
$\frac{\textsf{₹ } 17}{10 \text{ tablets}} = \frac{\textsf{₹ } C}{30 \text{ tablets}}$
... (i)
$\frac{17}{10} = \frac{C}{30}$
Multiply both sides by 30:
$C = \frac{17}{10} \times 30$
$C = 17 \times \frac{30}{10}$
$C = 17 \times \cancel{3}$
$C = 51$.
The total cost is $\textsf{₹}$ 51.
Shivangi will be required to pay $\textsf{₹}$ 51 for her medical bill for 15 days.
The final answer is $\textsf{₹}$ 51.
Question 83. The quarterly school fee in Kendriya Vidyalaya for Class VI is Rs 540. What will be the fee for seven months?
Answer:
Given:
Quarterly school fee = $\textsf{₹}$ 540
A quarter consists of 3 months.
So, the fee for 3 months is $\textsf{₹}$ 540.
Assume the fee is calculated at a uniform monthly rate.
To Find:
The school fee for seven months.
Solution:
First, find the fee per month.
Fee per month = $\frac{\text{Quarterly fee}}{\text{Number of months in a quarter}}$
Fee per month = $\frac{\textsf{₹ } 540}{3 \text{ months}}$
Calculate the division:
$\frac{540}{3}$
$540 \div 3 = (300 + 240) \div 3 = 300 \div 3 + 240 \div 3 = 100 + 80 = 180$.
Fee per month = $\textsf{₹}$ 180.
Now, use the fee per month to find the fee for seven months.
Fee for seven months = Fee per month $\times$ Number of months
Fee for seven months = $\textsf{₹ } 180 \text{/month} \times 7 \text{ months}$
Fee for seven months = $\textsf{₹ } (180 \times 7)$.
$180 \times 7 = 18 \times 10 \times 7 = 18 \times 70 = 1260$.
Fee for seven months = $\textsf{₹}$ 1260.
Alternatively, using proportion:
Let $F$ be the fee for 7 months.
The ratio of fee to number of months is constant.
$\frac{\text{Fee}_1}{\text{Months}_1} = \frac{\text{Fee}_2}{\text{Months}_2}$
$\frac{\textsf{₹ } 540}{3 \text{ months}} = \frac{\textsf{₹ } F}{7 \text{ months}}$
... (i)
$\frac{540}{3} = \frac{F}{7}$
Simplify the left side: $\frac{540}{3} = 180$.
$180 = \frac{F}{7}$
Multiply both sides by 7:
$F = 180 \times 7$
$F = 1260$.
The fee is $\textsf{₹}$ 1260.
The fee for seven months will be $\textsf{₹}$ 1260.
The final answer is $\textsf{₹}$ 1260.
Question 84. In an election, the votes cast for two of the candidates were in the ratio 5 : 7. If the successful candidate received 20734 votes, how many votes did his opponent receive?
Answer:
Given:
Ratio of votes for two candidates = 5 : 7
The successful candidate received 20734 votes.
To Find:
The number of votes received by the opponent.
Solution:
Let the number of votes received by the two candidates be in the ratio $5k : 7k$, where $k$ is a common factor.
Since the ratio is 5:7, the candidate who received more votes is the successful one. The larger part of the ratio is 7.
So, the successful candidate received votes corresponding to 7 parts, and the opponent received votes corresponding to 5 parts.
Number of votes for successful candidate = $7k$
Number of votes for opponent = $5k$
We are given that the successful candidate received 20734 votes.
$7k = 20734$
... (i)
Solve for $k$ by dividing both sides by 7:
$k = \frac{20734}{7}$
Perform the division:
$\begin{array}{r} 2962 \\ 7{\overline{\smash{\big)}\,20734}} \\ \underline{-~\phantom{()}(14)}\phantom{000} \\ 67\phantom{00} \\ \underline{-~\phantom{()}(63)}\phantom{00} \\ 43\phantom{0} \\ \underline{-~\phantom{()}(42)}\phantom{0} \\ 14 \\ \underline{-~\phantom{()}(14)} \\ 0 \end{array}$
$k = 2962$.
Now, find the number of votes received by the opponent, which is $5k$.
Number of votes for opponent = $5 \times 2962$.
Calculate the multiplication:
$\begin{array}{cc}& & 2 & 9 & 6 & 2 \\ \times & & & & & 5 \\ \hline & 1 & 4 & 8 & 1 & 0 \\ \hline \end{array}$
Number of votes for opponent = 14810.
The opponent received 14810 votes.
The final answer is 14810 votes.
Question 85. A metal pipe 3 metre long was found to weigh 7.6 kg. What would be the weight of the same kind of 7.8 m long pipe?
Answer:
Given:
Length of the first pipe = 3 m
Weight of the first pipe = 7.6 kg
Length of the second pipe = 7.8 m
The pipes are of the same kind, implying uniform density.
To Find:
The weight of the 7.8 m long pipe.
Solution:
Since the pipes are of the same kind, their weight is directly proportional to their length. This means the ratio of weight to length is constant.
We can find the weight per unit length (weight per meter).
Weight per meter = $\frac{\text{Weight of the first pipe}}{\text{Length of the first pipe}}$
Weight per meter = $\frac{7.6 \text{ kg}}{3 \text{ m}}$
Weight per meter = $\frac{7.6}{3}$ kg/m.
Now, use this weight per meter to find the weight of the 7.8 m long pipe.
Weight of the second pipe = Weight per meter $\times$ Length of the second pipe
Weight of the second pipe = $\frac{7.6}{3} \text{ kg/m} \times 7.8 \text{ m}$
Weight of the second pipe = $\frac{7.6 \times 7.8}{3}$ kg.
Calculate the expression:
$\frac{7.6 \times 7.8}{3}$
Notice that 7.8 is divisible by 3: $7.8 \div 3 = 2.6$.
Weight of the second pipe $= 7.6 \times 2.6$ kg.
Calculate the multiplication $7.6 \times 2.6$:
$\begin{array}{cc}& & 7 & . & 6 \\ \times & & 2 & . & 6 \\ \hline && 4 & 5 & 6 \\ & 1 & 5 & 2 & \times \\ \hline & 1 & 9 & . & 7 & 6 \\ \hline \end{array}$
Weight of the second pipe = 19.76 kg.
Alternatively, using proportion:
Let $W$ be the weight of the 7.8 m long pipe.
The ratio of weight to length is constant:
$\frac{\text{Weight}_1}{\text{Length}_1} = \frac{\text{Weight}_2}{\text{Length}_2}$
$\frac{7.6 \text{ kg}}{3 \text{ m}} = \frac{W \text{ kg}}{7.8 \text{ m}}$
... (i)
$\frac{7.6}{3} = \frac{W}{7.8}$
Multiply both sides by 7.8:
$W = \frac{7.6}{3} \times 7.8$
$W = 7.6 \times \frac{7.8}{3}$
$W = 7.6 \times 2.6$
$W = 19.76$ kg.
The weight of the 7.8 m long pipe would be 19.76 kg.
The final answer is 19.76 kg.
Question 86. A recipe for raspberry jelly calls for 5 cups of raspberry juice and $2\frac{1}{2}$ cups of sugar. Find the amount of sugar needed for 6 cups of the juice?
Answer:
Given:
Recipe requires 5 cups of raspberry juice and $2\frac{1}{2}$ cups of sugar.
Assume the ratio of sugar to juice is constant for the recipe.
To Find:
The amount of sugar needed for 6 cups of raspberry juice.
Solution:
First, convert the mixed number for the amount of sugar into an improper fraction:
$2\frac{1}{2} = 2 + \frac{1}{2} = \frac{4}{2} + \frac{1}{2} = \frac{4+1}{2} = \frac{5}{2}$ cups.
The recipe gives a ratio of sugar to raspberry juice.
Ratio of sugar to juice = Amount of sugar : Amount of juice
Ratio = $\frac{5}{2}$ cups : 5 cups.
We can write this as a fraction:
Ratio = $\frac{5/2}{5} = \frac{5}{2 \times 5} = \frac{\cancel{5}^{1}}{2 \times \cancel{5}_{1}} = \frac{1}{2}$.
The ratio of sugar to juice is 1:2.
Now, we need to find the amount of sugar needed for 6 cups of juice, maintaining the same ratio. Let $S$ be the amount of sugar needed (in cups) for 6 cups of juice.
The ratio of sugar to juice is constant:
$\frac{\text{Amount of sugar}_1}{\text{Amount of juice}_1} = \frac{\text{Amount of sugar}_2}{\text{Amount of juice}_2}$
$\frac{\text{5/2 cups}}{\text{5 cups}} = \frac{S \text{ cups}}{6 \text{ cups}}$
... (i)
Using the simplified ratio $\frac{1}{2}$:
$\frac{1}{2} = \frac{S}{6}$
... (ii)
Solve for $S$ by multiplying both sides of the equation by 6:
$S = \frac{1}{2} \times 6$
$S = \frac{6}{2}$
$S = 3$
So, 3 cups of sugar are needed for 6 cups of raspberry juice.
The final answer is 3 cups.
Question 87. A farmer planted 1890 tomato plants in a field in rows each having 63 plants. A certain type of worm destroyed 18 plants in each row. How many plants did the worm destroy in the whole field?
Answer:
Given:
Total number of tomato plants = 1890
Number of plants in each row = 63
Number of plants destroyed by worm in each row = 18
To Find:
The total number of plants destroyed in the whole field.
Solution:
First, find the total number of rows in the field.
Total number of plants = Number of rows $\times$ Number of plants per row.
Number of rows = $\frac{\text{Total number of plants}}{\text{Number of plants per row}}$
Number of rows = $\frac{1890}{63}$.
Calculate the division:
$\frac{1890}{63}$
Divide 189 by 63. $63 \times 3 = 189$.
So, $\frac{189}{63} = 3$.
$\frac{1890}{63} = \frac{189 \times 10}{63} = 3 \times 10 = 30$.
Number of rows = 30.
The worm destroyed 18 plants in each row.
Total number of plants destroyed = Number of rows $\times$ Number of plants destroyed per row
Total number of plants destroyed = $30 \times 18$.
Calculate the multiplication $30 \times 18$:
$30 \times 18 = 3 \times 10 \times 18 = 3 \times 18 \times 10 = 54 \times 10 = 540$.
Total number of plants destroyed = 540.
Alternatively, using ratio/proportion on the number of plants destroyed per row:
In each row of 63 plants, 18 plants are destroyed.
The fraction of plants destroyed per row is $\frac{18}{63}$. Simplify this fraction: $\frac{18 \div 9}{63 \div 9} = \frac{2}{7}$.
This means $\frac{2}{7}$ of the plants are destroyed in the whole field.
Total number of plants destroyed = Fraction destroyed $\times$ Total number of plants
Total number of plants destroyed = $\frac{2}{7} \times 1890$.
$\frac{2}{7} \times 1890 = 2 \times \frac{1890}{7}$
$1890 \div 7 = (1400 + 490) \div 7 = 1400 \div 7 + 490 \div 7 = 200 + 70 = 270$.
Total number of plants destroyed = $2 \times 270 = 540$.
The worm destroyed 540 plants in the whole field.
The final answer is 540 plants.
Question 88. Length and breadth of the floor of a room are 5m and 3m, respectively. forty tiles, each with area $\frac{1}{16}$ m2 are used to cover the floor partially. Find the ratio of the tiled and the non tiled portion of the floor.
Answer:
Given:
Dimensions of the room floor: Length = 5 m, Breadth = 3 m
Number of tiles used = 40
Area of each tile = $\frac{1}{16}$ m$^2$
To Find:
The ratio of the tiled portion to the non-tiled portion of the floor.
Solution:
First, calculate the total area of the floor of the room.
Area of floor = Length $\times$ Breadth
Area of floor = $5 \text{ m} \times 3 \text{ m} = 15 \text{ m}^2$.
Next, calculate the total area covered by the tiles (tiled portion).
Area of tiled portion = Number of tiles $\times$ Area of each tile
Area of tiled portion = $40 \times \frac{1}{16}$ m$^2$.
Area of tiled portion = $\frac{40}{16}$ m$^2$.
Simplify the fraction $\frac{40}{16}$ by dividing the numerator and denominator by their GCD, which is 8.
$\frac{40 \div 8}{16 \div 8} = \frac{5}{2}$
Area of tiled portion = $\frac{5}{2} = 2.5$ m$^2$.
Now, calculate the area of the non-tiled portion of the floor.
Area of non-tiled portion = Total area of floor - Area of tiled portion
Area of non-tiled portion = $15 \text{ m}^2 - 2.5 \text{ m}^2 = 12.5 \text{ m}^2$.
Finally, find the ratio of the tiled portion to the non-tiled portion of the floor.
Ratio = Area of tiled portion : Area of non-tiled portion
Ratio = 2.5 m$^2$ : 12.5 m$^2$
Ratio = 2.5 : 12.5.
To express this ratio with whole numbers, multiply both terms by 10:
Ratio = $2.5 \times 10 : 12.5 \times 10$
Ratio = 25 : 125.
Simplify the ratio 25:125 by dividing both numbers by their GCD, which is 25.
Ratio = $\frac{25 \div 25}{125 \div 25} = \frac{1}{5}$.
The ratio is 1:5.
The ratio of the tiled and the non-tiled portion of the floor is 1:5.
The final answer is 1:5.
Question 89. A carpenter had a board which measured 3m × 2m. She cut out a rectangular piece of 250 cm × 90 cm. What is the ratio of the area of cut out piece and the remaining piece?
Answer:
Given:
Dimensions of the original board = 3 m $\times$ 2 m
Dimensions of the cut-out piece = 250 cm $\times$ 90 cm
To Find:
The ratio of the area of the cut-out piece to the area of the remaining piece.
Solution:
To calculate and compare areas, the dimensions must be in the same unit. Let's convert the dimensions of the original board from meters to centimeters.
We know that $1 \text{ meter} = 100 \text{ centimeters}$.
Length of the original board = $3 \text{ m} = 3 \times 100 \text{ cm} = 300 \text{ cm}$.
Breadth of the original board = $2 \text{ m} = 2 \times 100 \text{ cm} = 200 \text{ cm}$.
Now, calculate the area of the original board.
Area of original board = Length $\times$ Breadth
Area of original board = $300 \text{ cm} \times 200 \text{ cm} = 60000 \text{ cm}^2$.
Calculate the area of the cut-out rectangular piece.
Area of cut-out piece = Length $\times$ Breadth
Area of cut-out piece = $250 \text{ cm} \times 90 \text{ cm}$.
$250 \times 90 = 250 \times (100 - 10) = 25000 - 2500 = 22500$.
Area of cut-out piece = 22500 $\text{ cm}^2$.
Calculate the area of the remaining piece of the board.
Area of remaining piece = Area of original board - Area of cut-out piece
Area of remaining piece = $60000 \text{ cm}^2 - 22500 \text{ cm}^2 = 37500 \text{ cm}^2$.
Find the ratio of the area of the cut-out piece to the area of the remaining piece.
Ratio = Area of cut-out piece : Area of remaining piece
Ratio = 22500 $\text{ cm}^2$ : 37500 $\text{ cm}^2$.
Write the ratio as a fraction and simplify:
Ratio = $\frac{22500}{37500}$
Cancel out the common zeros:
Ratio = $\frac{225}{375}$
Divide both the numerator and denominator by their greatest common divisor (GCD). Both are divisible by 25.
$\frac{225 \div 25}{375 \div 25} = \frac{9}{15}$
Now divide both the numerator and denominator by their GCD, which is 3.
$\frac{9 \div 3}{15 \div 3} = \frac{3}{5}$
The ratio is 3:5.
The ratio of the area of cut-out piece and the remaining piece is 3:5.
The final answer is 3:5.

